目次
背景・目的
今までに書いてきたこれらの記事では、
ロボットの制御モデルを状態空間モデル
という形式で表現していましたが、
もう一つの形式として伝達関数モデルが
あります。これまでに大学の授業などで
伝達関数については触れた事もありますが、
それが結局何の役に立つのかが全然分かって
いませんでした。
今回改めて勉強し直したので、それについて
メモしておきます。
伝達関数とは
制御対象のシステムに与える入力と、その
結果得られる出力の関係を表した関数で、
入出力システムの挙動や安定性を評価する
ためのものです。
このような入出力の関係を表す関数には、
入力信号の種類に関係なく要素固有の関数
となる事が要求されます。
ここで言う要素とは、入力の設定部やセンサ
による検出部、必要な制御入力を作る調節部、
といったものであり、それらは制御要素または
単に要素と呼ばれます。
時間領域とs領域
伝達関数についての理解を難しくさせる
一番のポイントはこれではないでしょうか。
少なくとも自分はこれのせいでチンプンカンプン
でした。
例えば、こちらのようなsin波形やステップ状
波形をシステムの入力として与える場合、
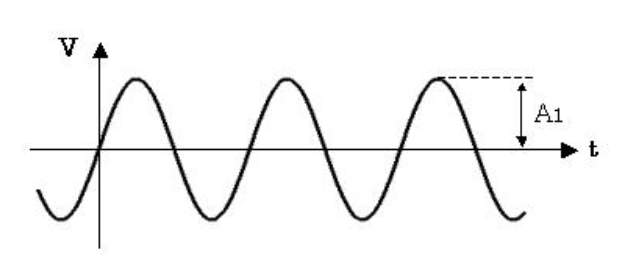

入力信号は時間0からある時間tまでの間で
変化するため、それに対する出力信号も
時間0からtまでの間で変化するものになり
ます。
時間領域のまま入力と出力の関係を表す
関数を定義した場合、それは時間の積分の
計算を必要とする面倒な形となって
しまいます。
そのため、元の時間関数をf(t)として、
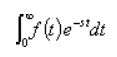
のように「時間t=0から∞まで積分する」と
いう数学的加工を施すラプラス変換により、
s領域というシンプルな形で表します。
これにより、例えばこのような入出力システムを
考える場合、
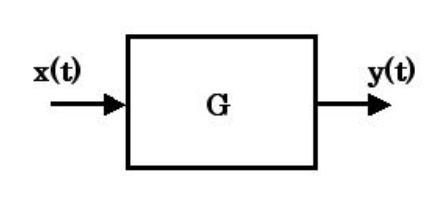
ラプラス変換を施した際のx(t), y(t), Gの関係は、
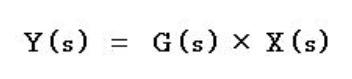
となり、この式中のG(s)が伝達関数と呼ばれます。
時間領域からs領域への変換
時間領域のt関数で表された状態空間モデルを
s領域のs関数で表された伝達関数モデルに変換
するには、こちらの式を用います。
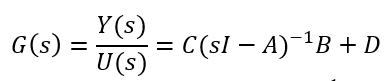
Y(s)が出力、U(s)が入力、A, B, C, Dは状態空間
モデル内の各行列であり、こちらのように
定義します。
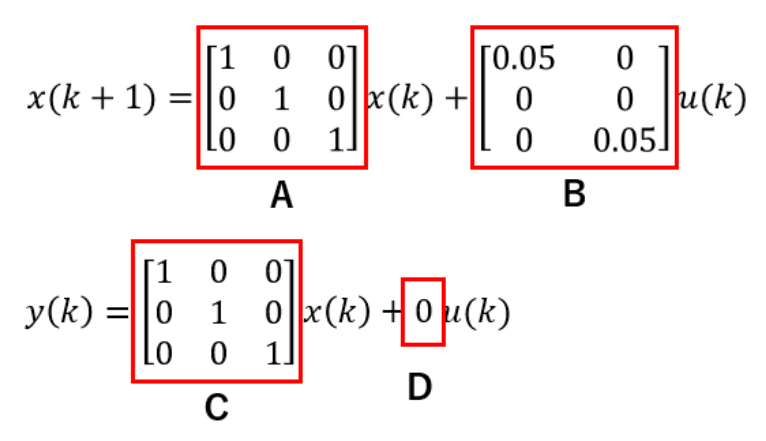
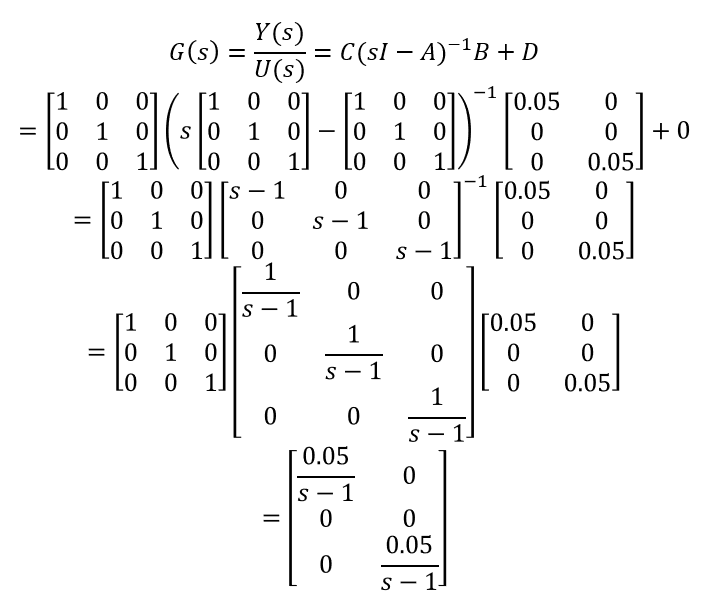
そして、この状態空間モデルから伝達関数
モデルへの変換は、こちらのような計算で
求める事が出来ます。
ちなみに、この計算の中に含まれる逆行列の
計算はこちらのようになります。
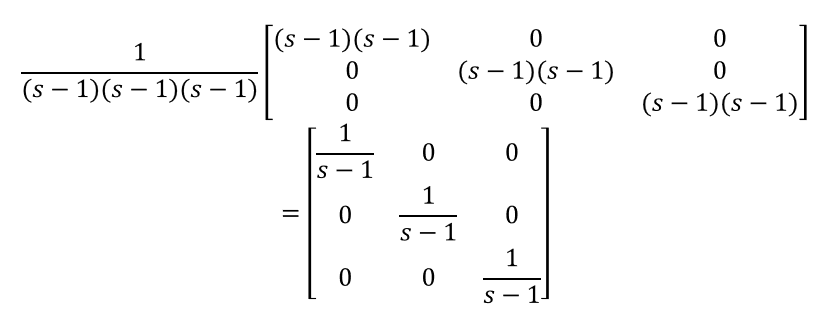
伝達関数モデルは1入力1出力を表すものなので、
今回のような多入力多出力の状態空間モデルから
変換した場合は、入力ベクトルの各要素と出力
ベクトルの各要素の組み合わせ毎に伝達関数が
求められる事になります。
Pythonサンプルプログラム
上記の状態空間モデルから伝達関数モデルに
変換するPythonプログラムを作りました。
""" Conversion sample from state space model to transfer function model State equation example x(t+1) = A * x(t) + B * u(t) A: 3 x 3 matrix B: 3 x 2 matrix Output equation example y(t) = C * x(t) + D * u(t) C: 3 x 3 matrix D: 0 Transfer function example 2-Input 3-Output author: Shisato Yano (@4310sy) """ import numpy as np from control.matlab import ss, ss2tf def define_state_space_model(A, B, C, D): ss_model = ss(A, B, C, D) return ss_model def convert_transfer_function_model(ss_model): tf_model = ss2tf(ss_model) return tf_model def main(): print("Run " + __file__) # define matrix A = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]]) B = np.array([[0.05, 0], [0, 0], [0, 0.05]]) C = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]]) D = 0 ss_model = define_state_space_model(A, B, C, D) tf_model = convert_transfer_function_model(ss_model) print('Converted transfer function model') print(tf_model) if __name__ == '__main__': main()
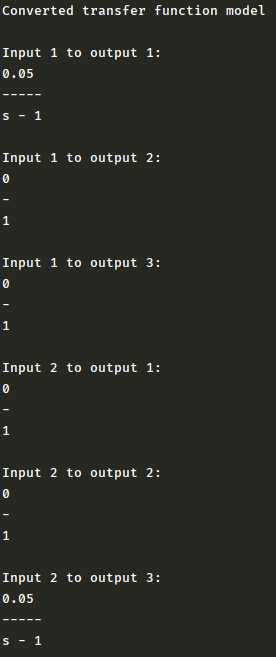
実行すると、こちらのように各入出力のペアにおける
伝達関数が計算されます。
GitHubリポジトリ
今回紹介したサンプルプログラムは、
こちらで公開しています。
