詳解　確率ロボティクス　Ｐｙｔｈｏｎによる基礎アルゴリズムの実装 (ＫＳ理工学専門書)

作者:上田隆一
発売日: 2019/12/20
メディア: Kindle版

はじめに

前回の記事では、
センサ値の度数分布を可視化して、
平均値や分散、標準偏差を計算
するJuliaコードを紹介しました。

www.eureka-moments-blog.com

それに続いて今回は、
各センサ値の頻度から確率分布を
計算し、そこから確率モデルを導出、
可視化するJuliaコードについて
紹介します。

GitHubリポジトリ

本記事で紹介するJuliaコードは全てこちらの
リポジトリにて公開しています。

github.com

頻度の集計

次のようなセンサ値のリストから
各センサ値の出やすさ(確率)を数値化
することで、 $N$ 回目以降に
観測されるセンサ値がどうなるかを
予測することができます。

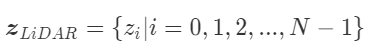
f:id:sy4310:20210409203836p:plain

そのためにまずは、各センサ値の
頻度を集計してみます。Juliaでは、
Freqtablesというパッケージがあり、
集計結果をテーブル形式で綺麗に
まとめて出力してくれます。

github.com

Juliaコードでこのパッケージを
使うために次のコードで取り込み
ます。

using FreqTables

そして、次のようにセンサデータを
読み込んで各センサ値の頻度を集計
します。

data_path = joinpath(split(@__FILE__, "src")[1], "data/sensor_data_200.txt")
df_200_mm = CSV.read(data_path, DataFrame, 
                     header=["date", "time", "ir", "lidar"],
                     delim=' ')
        
tbl = freqtable(df_200_mm.lidar)
println("FreqTable: $(tbl)")

一番最後の行が頻度を集計する
freqtable関数で、これを実行
すると、次のような出力が得られ
ます。
f:id:sy4310:20210411121615p:plain

左の列が集計対象の各センサ値、
右の列がそれぞれの頻度になります。
このとき、各センサ値に従って昇順に
勝手にソートしてくれるので便利です。

確率の計算

各センサ値の集計ができたので、
その結果から確率を計算してみます。
まずは次のコードで、先程の頻度
テーブルから頻度の値が入った列を
抽出します。

freqs = [value for(name, value) in enumerate(tbl)]
println("Frequency: $(freqs)")

Pythonでも御馴染みのenumerate関数を
使い、リスト内包表記で頻度値の配列を
生成しています。
f:id:sy4310:20210417214241p:plain

また、後で必要になるので、各頻度値に
対応するセンサ値も配列として用意して
おきます。

observs = [Int(obsv) for obsv in names(tbl, 1)]
println("Observations: $(observs)")

先程の頻度テーブルにおける左側の列が
そうなのですが、これはこのままでは
NamedArrayという特殊な形式の配列なので、
そのままplot関数への入力として使うことが
できません。
そのため、names関数でまずはString配列
として取り出し、それをさらにInt関数で
整数配列にしています。
f:id:sy4310:20210417215209p:plain

NamedArrayの扱い方については
こちらを参照ください。
github.com

そして、次のコードで各頻度値を
全データ数で割ることで、各センサ値の
発生確率を計算できます。

probs = freqs ./ length(df_200_mm.lidar)
println("Probability: $(probs)")

f:id:sy4310:20210417223233p:plain

最後に、計算した確率を次のコードで
可視化してみます。

bar(probs, xticks=observs, label="prob dist")

Plotsパッケージに含まれるbar関数に、
入力として計算した確率値の配列を、
xticks引数で各センサ値に合わせて
x軸を刻むように指定します。
f:id:sy4310:20210417224638p:plain
このように、前回の記事で描いた
ヒストグラムと似たグラフが描けますが、
縦軸は頻度ではなく確率になっている
ことが分かります。

確率質量関数

上記の確率は、個別の確率 $P(z)$ を
与える関数 $P$ 全体を描いたものであり、
確率質量関数といいます。
各変数に対して確率がどう分布するか
を表す実体が $P$ と考えることも
でき、確率分布と呼ばれます。

確率モデル

今度は、ここまでに求めてきたセンサ値の
分布をモデル化してみます。これにより、
実際のセンサデータが無くても、センサ値
の発生をシミュレーションできるように
なります。

ガウス分布の当てはめ

先に示したようなセンサ値の頻度や確率の
分布からして、これはガウス分布に従って
いると考えられます。
ガウス分布の確率密度関数は次式のように
なり、
f:id:sy4310:20210418214854p:plain
前回の記事で計算したセンサ値の分散を
$\sigma ^2$ に、平均値を $\mu$ に代入することで、
特定のセンサ値が得られる確率を計算
できます。これをJuliaコードで実装すると
次のようになります。

function p(z, mu=209.7, dev=23.4)
    return exp(-(z - mu)^2 / (2 * dev)) / sqrt(2 * pi * dev)
end

実際に得られるセンサ値の範囲が190~230と
して、上式を次のコードで描画してみましょう。

zs = Array(190:230)
ys = [p(z) for z in zs]

plot(zs, ys, label="gaussian distribution")

このようなグラフが描画されるはずです。
f:id:sy4310:20210418233558p:plain
すでに作成したヒストグラムと似た形状に
なっていることが分かります。

続いて、先程の確率密度関数を
積分し、センサ値が整数に限定
される離散的な確率分布を作って
みます。
各センサ値 $x$ を区間 $[x-0.5, x+0.5$ ]
の範囲で積分するとし、コードは
次のようになります。

function prob(z, width=0.5)
    return width * (p(z - width) + p(z + width))
end

zs = Array(193:229)
ys = [prob(z) for z in zs]

bar(ys, xticks=zs, color=:red, alpha=0.3, label="Model")
bar!(probs, xticks=observs, color=:blue, alpha=0.3, label="Observations")

このコードでは、確率密度関数の
積分から求めた確率分布と、先に
センサ値の頻度から求めた確率分布
を重ね合わせた棒グラフを描画します。
f:id:sy4310:20210418235602p:plain
赤が積分から求めた確率分布で、
青がセンサ値の頻度から求めた
確率分布ですが、ちゃんと実際の
センサ値の傾向に近い形状でモデル化
できている事が分かります。

確率密度関数

先に示したコードではガウス分布の
確率密度関数の数式を自前で実装
しましたが、Distributionパッケージで
用意されているpdf関数を使えば、次の
ようにより簡単なコードで実現できます。

using Plots, Distributions
pyplot()

norm_dist = Normal(209.7, 4.84) # mu, std_dev

zs = Array(193:229)
ys = [pdf(norm_dist, z) for z in zs]
plot(zs, ys, label="PDF")

まずこのコードの4行目では、Normal関数を
使って正規分布オブジェクトを生成して
います。第一引数が平均値、第2引数が標準
偏差です。
続いて6行目で193から229までの疑似的な
センサ値配列を定義、これを7行目でpdf関数
に入力して確率分布を計算しています。
pdf関数は確率密度関数であり、第一引数には
4行目で生成したような分布オブジェクト、
第二引数には今回のセンサ値のような変数 $x$ に
あたるデータを与えます。

このコードにより、先程のグラフと同じ形状の
ものが描画されるはずです。
f:id:sy4310:20210420225350p:plain

累積分布関数

こういった確率密度分布は積分すると
1になるわけですが、その傾向がより
分かりやすい累積分布関数というもの
もあります。

bellcurve.jp

f:id:sy4310:20210420230243p:plain

これは、変数 $z$ が $a$ 以下となる確率 $P(z)$ を
全て足し合わせたものであり、これを
全センサ値に対して計算すると、次の
ようなグラフを描画できます。

norm_dist = Normal(209.7, 4.84) # mu, std_dev

zs = Array(193:229)
ys = [cdf(norm_dist, z) for z in zs]
plot(zs, ys, color=:red, label="CDF")

f:id:sy4310:20210421220010p:plain

先に示した確率密度関数のコードと同様に、
まずは1行目で正規分布オブジェクトを
生成し、それをcdf関数の引数として与える
ことで累積分布関数を計算します。
グラフを見ると、各センサ値における確率
が計算されながら積算され、最終的には
1になるのが分かります。

期待値

期待値とは、ある分布 $P$ について $z \sim P(z)$ を
無限に繰り返した場合に、 $z$ の平均値がどの程度に
なるかを示すものです。

この $z$ が離散的な場合は、
f:id:sy4310:20210422220151p:plain

連続的な場合は、
f:id:sy4310:20210422220744p:plain

という数式で表されます。

例えば、6面のサイコロを10000回振って
出る値の平均をとることで期待値を近似的に
求めることができます。そのときのJulia
コードは次のようになります。

samples = rand(1:6, 10000)
exp_value = sum(samples) / length(samples)
println("Random sampling 10000 times with 6 sided dice")
println("Expected value = $(exp_value)")

1行目で1~6の範囲で乱数を10000個生成
し、その平均を2行目で計算しています。
これを実行すると、次のような出力が
得られます。
f:id:sy4310:20210422223037p:plain

まとめ

今回の記事では、センサ値の確率分布を
計算するJuliaコードを紹介しました。

扱ったのは主に正規分布でしたが、
実際はもっと複雑な形状の分布と
なるセンサ値が得られるような状況も
多くあり、それらをモデル化するには
またいろいろな前処理のテクニックが
必要になります。

次回は、そういった複雑な分布の
モデル化について紹介していきます。

EurekaMoments

ロボットや自動車の自律移動に関する知識や技術、プログラミング、ソフトウェア開発について勉強したことをメモするブログ

Juliaで学ぶ確率ロボティクス～センサ値の確率分布～

目次