
- 作者:裕樹, 南
- 発売日: 2019/05/22
- メディア: 単行本
目次
背景・目的
ここ最近、制御工学を勉強したい熱が高まって
きたので早速取り組み始めました。主に、
ロボットの自律移動や車の自動運転のための
制御を学んでいきます。
今回は記念すべき第1回。移動ロボットとして
一般的な、対向2輪型ロボットを制御するための
運動モデルの定義と、その動作を学ぶための
Pythonサンプルプログラムについて書きます。
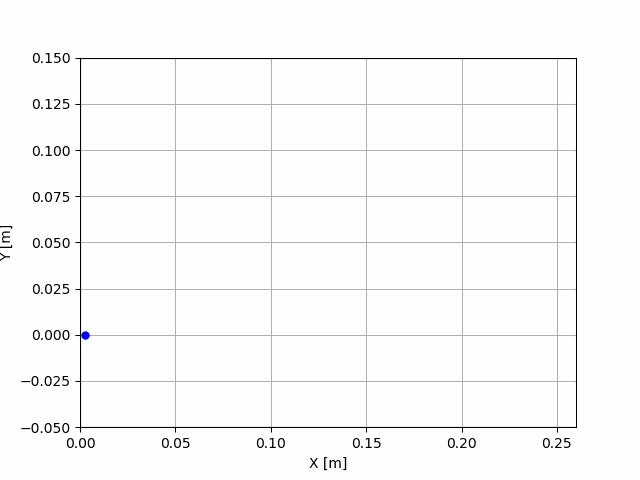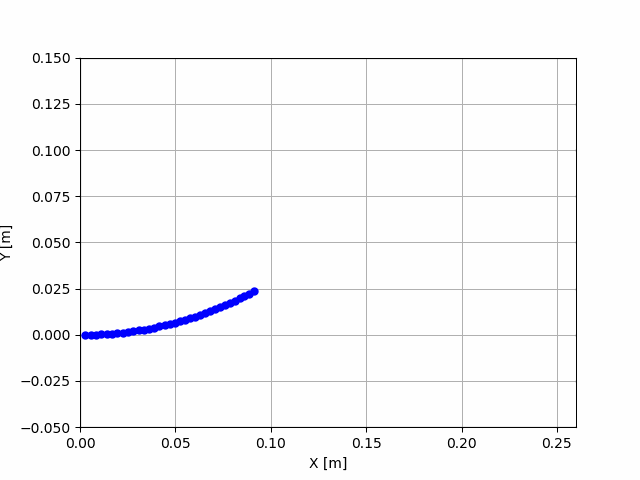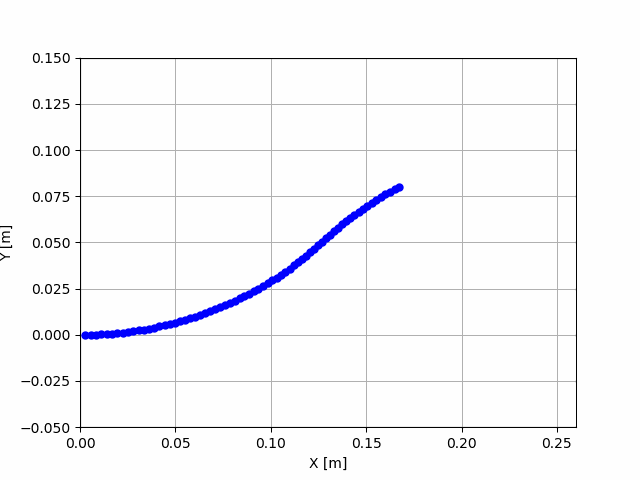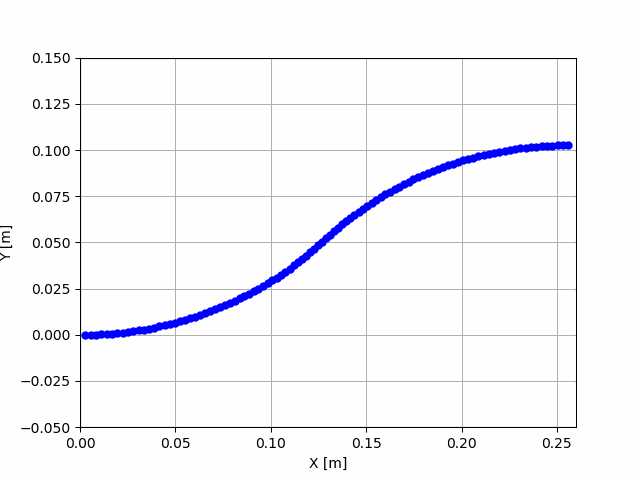
対向2輪型ロボット
2個の車輪を左右対称にロボットに取り付け、
それぞれを独立に駆動する形態であり、両輪
の回転によって制御されます。
 図中の文字は、それぞれ下記を定義したもの
図中の文字は、それぞれ下記を定義したもの
になります。

モデル化
ロボットを制御するためには、その特徴を
数学的に捉えたモデルを作る必要があります。
世の中の制御対象の多くは動的なシステム
であり、現在の出力に過去の入力が関係する
システムです。
ここでは、システムに与える入力、得られる
出力、システムの状態を表す状態変数を
定義して、これらを一つの式でまとめた
状態空間モデルという形で表現します。
前提条件
車輪移動ロボットの動作を数学的にモデル化
する際、それをシンプルで理解しやすいもの
とするために、「車輪は滑らない」という
前提の元でモデル化するのが一般的です。
車輪が滑らないとした場合、下記の事が言える
ようになり、ロボットの挙動が理解しやすく
なります。
- 車輪は車軸に垂直な方向にしか移動しない。
- 車軸方向へのドリフトはしない。
- 運動中は、各瞬間で旋回中心が存在する。
- 全ての車軸の回転軸は旋回中心を通る。
状態変数の定義
状態変数とは、任意の時点におけるシステム
全体の状態を表せる変数群の最小の部分集合
の事です。今回のような移動ロボットの場合、
ロボットの位置座標と方位角とするのが一般
的であり、それらを下記のようなベクトルの
形で表現します。

入力の定義
車輪移動ロボットを動かすための入力は、
一般には進行方向速度vと旋回角速度ω
です。
この時、左右車輪の回転角速度がエンコーダ
などのセンサで取得できるとした場合、
入力vとωはロボットのトレッドと車輪半径
も考慮して下記のような式で決定されます。

出力の定義
ロボットの制御プログラムは、基本的
には一定の時間間隔で車輪のエンコーダ
などの情報を読み取り処理を行う事から、
離散的で時変なシステムと考える事が
出来ます。
これに従い、状態空間モデルは下記の
ように定義されます。

上段の式を状態方程式、下段の式を
出力方程式と呼びます。
ある時刻kにおけるx(k)を状態ベクトル、
y(k)を出力ベクトル、u(k)を入力ベクトル
と呼びます。
また、A(k)を状態行列、B(k)を入力行列、
C(k)を出力行列、D(k)を直達行列と
呼びます。
ただし、大抵の場合は単純化するために、
直達行列D(k)は零行列とする、つまり
システムには直達項が無いものとして
扱う事が多いです。
以上を踏まえて、今回の2輪ロボットの
状態方程式は下記のようになります。

また出力方程式は、基本的には状態ベクトル
x(k)がそのままシステムとしての出力となる
ので、

となります。
Pythonプログラム
上記のモデルによりロボットがどのように
振る舞うかをシミュレートするサンプル
プログラムをPythonで作りました。
システムに与える入力は、前半5秒は
右車輪の回転速度を速くして左旋回、
後半5秒は左車輪の回転速度を速くして
右旋回させるようにしています。
このプログラムを実行すれば、記事の冒頭に
載せているような移動シミュレーションが
実行されます。
""" Two wheel motion model sample author: Shisato Yano (@4310sy) """ import numpy as np from math import cos, sin import matplotlib.pyplot as plt from PIL import Image import os show_plot = True DELTA_TIME = 0.1 # time tick [s] SIM_TIME = 10 # simulation time [s] class TwoWheelModel: def __init__(self, tr, td): """ Initialize two wheel model tr: tire radius [m] td: tread [m] """ self.tire_radius_m = tr self.tread_m = td def calculate_input(self, tasr, tasl): """ tasr: tire angular speed right [rad/s] tasl: tire angular speed left [rad/s] :return: speed input [m/s], yaw rate input [rad/s] """ mat = np.array([[self.tire_radius_m/2, self.tire_radius_m/2], [self.tire_radius_m/self.tread_m, -self.tire_radius_m/self.tread_m]]) vec = np.array([[tasr], [tasl]]) input_vec = np.dot(mat, vec) return input_vec def control_input(self, time): if time <= 5.0: tasr = 0.6 # [rad/s] tasl = 0.1 # [rad/s] else: tasr = 0.1 # [rad/s] tasl = 0.6 # [rad/s] input_vec = self.calculate_input(tasr, tasl) return input_vec def output_equation(self, state, input_vec): out_mat = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]]) dirc_mat = np.array([[cos(state[2, 0]) * DELTA_TIME, 0], [sin(state[2, 0]) * DELTA_TIME, 0], [0, DELTA_TIME]]) out_vec = np.dot(out_mat, state) + np.dot(dirc_mat, input_vec) return out_vec def create_gif(self, im_num): images = [] for num in range(im_num): im_name = str(num) + '.png' im = Image.open(im_name) images.append(im) os.remove(im_name) images[0].save('TwoWheelModel.gif', save_all=True, append_images=images[1:], loop=0, duration=60) def main(): print("Run " + __file__) # set parameters tire_radius_m = 0.08 tread_m = 0.26 # initialize two_wheel = TwoWheelModel(tire_radius_m, tread_m) # elapsed time time = 0.0 # state vector: x, y, yaw st_vec = np.zeros((3, 1)) # figure ax_xy = plt.subplot(1, 1, 1) plt_xy, = ax_xy.plot([], [], '.', c='b', ms=10) ax_xy.set_xlim([0.0, 0.26]) ax_xy.set_ylim([-0.05, 0.15]) ax_xy.set_xlabel("X [m]") ax_xy.set_ylabel("Y [m]") ax_xy.grid(True) # image number im_num = 0 # simulation st_x = [] st_y = [] st_yaw = [] while SIM_TIME >= time: time += DELTA_TIME input_vec = two_wheel.control_input(time) st_vec = two_wheel.output_equation(st_vec, input_vec) st_x.append(st_vec[0, 0]) st_y.append(st_vec[1, 0]) st_yaw.append(st_vec[2, 0]) if show_plot: plt_xy.set_data(st_x, st_y) plt.savefig(str(im_num) + '.png') im_num += 1 plt.pause(0.001) if im_num > 0: two_wheel.create_gif(im_num) if show_plot: plt.plot(st_x, st_y, ".b") plt.grid(True) plt.axis("equal") plt.xlabel("X [m]") plt.ylabel("Y [m]") plt.show() if __name__ == '__main__': main()
GitHubリポジトリ
上記のコードは、こちらのGitHub
リポジトリで公開しています。