
- 作者:森 泰親
- 発売日: 2014/10/04
- メディア: 単行本(ソフトカバー)
目次
背景・目的
以前の記事にて2輪型ロボットの制御モデルについて
書きました。
こうやってモデル化されたシステムが、ある入力に
よってある状態に持っていけるものである事を
可制御、何かしらの方法でどういう状態である事を
可観測といい、これらを判定する事は重要です。
今回は、可制御・可観測の判定手法を勉強したので、
その手法と、それを実行するPythonサンプルサンプル
プログラムについて紹介します。
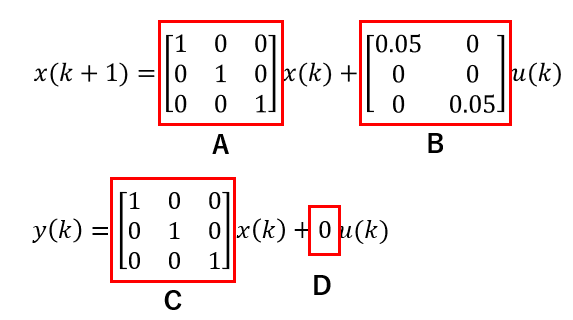
判定対象とするモデル
以前の記事で定義した状態空間モデルに基づいて、
状態方程式
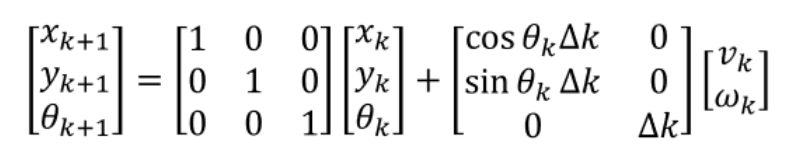
出力方程式
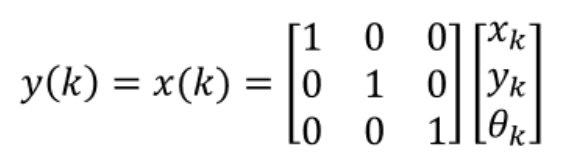
こちらのシステムを対象に、可制御と可観測を
説明していきます。
事前知識
システムの可制御、可観測を判定するには、
モデルの行列A, B, Cを用いて行列の階数
(ランク)を計算する必要があります。
ランクについてはこちらの記事がとても
分かりやすいので参照して頂きたいの
ですが、
ランクとは、ある行列Aを簡約化した行列を
Bとした時、その中で零ベクトルでない行の
数の事です。
また、行列Bの中で1次独立な列ベクトルの
最大数であり、1次独立な行ベクトルの最大数
でもあります。
そして、この行列Bの行数nに対してランクの
数が小さい場合は「ランク落ちしている」と
いう表現をします。
この「ランク落ちしている」か「していない」か
が分かるメリットとして、元の行列Aが逆行列を
持つか否か知る事が出来ます。
ロボットの制御や状態推定などにおいて、逆行列の
計算は必要不可欠なものです。逆行列の存在を知る
手段の一つとして覚えておくべきかと思います。
可制御の判定とサンプルプログラム
システムにおける各状態変数が、何かしらの
方法で制御可能である事を可制御といいます。
これを判定するには、先に定義した行列AとBを
用いて、
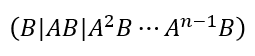
という可制御性行列を計算し、そのランクが
元の行数nと同じなら、そのシステムは可制御
であると言う事が出来ます。
今回のシステムの行列AとBから可制御性を
判定する、こちらのようなPythonプログラム
を作ってみました。
""" Controllability check sample State equation example x(t+1) = A * x(t) + B * u(t) A: 3 x 3 matrix B: 3 x 2 matrix Output equation example y(t) = C * x(t) + D * u(t) C: 3 x 3 matrix D: 0 author: Shisato Yano (@4310sy) """ import numpy as np from control.matlab import ss, ctrb def define_state_space_model(A, B, C, D): ss_model = ss(A, B, C, D) print('State space model') print(ss_model) def check_controllability(A, B): cntrb_mat = ctrb(A, B) rank = np.linalg.matrix_rank(cntrb_mat) print('Controllability matrix') print(cntrb_mat) print('') print('Rank is', rank) print('') if rank != A.shape[0]: print('This system is not controllability\n') else: print('This system is controllability\n') def main(): print("Run " + __file__) # define matrix A = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]]) B = np.array([[0.05, 0], [0, 0], [0, 0.05]]) C = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]]) D = 0 define_state_space_model(A, B, C, D) check_controllability(A, B) if __name__ == '__main__': main()
これを実行すると、このようにランクを計算し、
可制御か否かを判定してくれます。
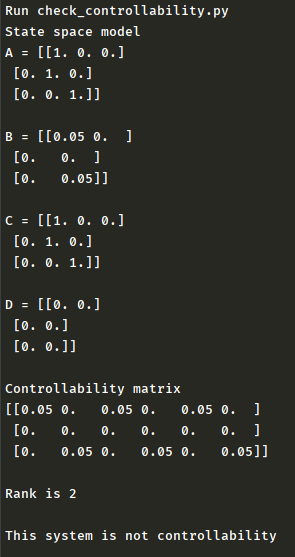
今回のシステムでは行列の行数n=3なので、
計算すべき可制御性行列は、

となり、これを簡約化した行列は、

赤丸の部分からランクは2であり、
可制御ではないという事になります。
システムが可制御であるためには、
目標とする状態に対する自分の状態の
変化を考慮して入力を決める必要が
ありますが、今回のシステムでは
そういうモデルにはなっていません。
なので、このシステムは可制御では
ないという事になります。
可観測の判定とサンプルプログラム
システムにおける各状態変数が、何かしらの
方法で観測可能である事を可観測といいます。
これを判定するには、先に定義した行列Aと
Cを用いて、

という可観測性行列を計算し、そのランクが
元の行数nと同じなら、そのシステムは可観測
であると言う事が出来ます。
今回のシステムの行列AとCから可観測性を
判定する、こちらのようなPythonプログラム
を作りました。
""" Observability check sample State equation example x(t+1) = A * x(t) + B * u(t) A: 3 x 3 matrix B: 3 x 2 matrix Output equation example y(t) = C * x(t) + D * u(t) C: 3 x 3 matrix D: 0 author: Shisato Yano (@4310sy) """ import numpy as np from control.matlab import ss, obsv def define_state_space_model(A, B, C, D): ss_model = ss(A, B, C, D) print('State space model') print(ss_model) def check_observability(A, C): obsv_mat = obsv(A, C) rank = np.linalg.matrix_rank(obsv_mat) print('Observability matrix') print(obsv_mat) print('') print('Rank is', rank) print('') if rank != A.shape[0]: print('This system is not observability\n') else: print('This system is observability\n') def main(): print("Run " + __file__) # define matrix A = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]]) B = np.array([[0.05, 0], [0, 0], [0, 0.05]]) C = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]]) D = 0 define_state_space_model(A, B, C, D) check_observability(A, C) if __name__ == '__main__': main()
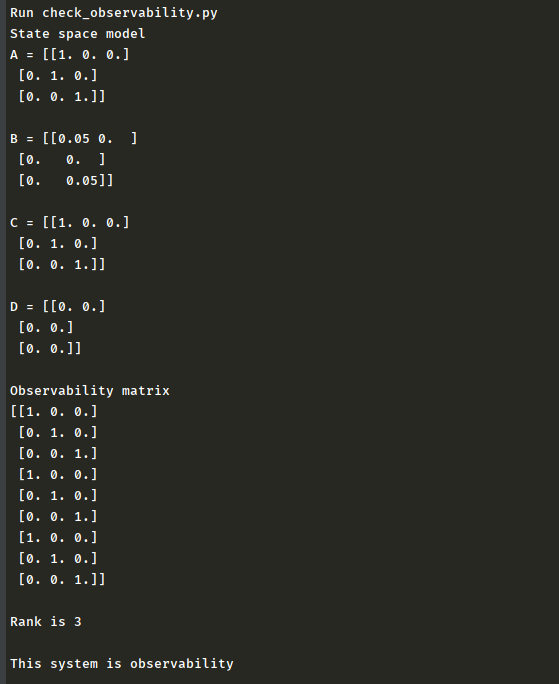
これを実行すると、先程の可制御判定と
同様にランクを計算し、可観測か否かを
判定してくれます。
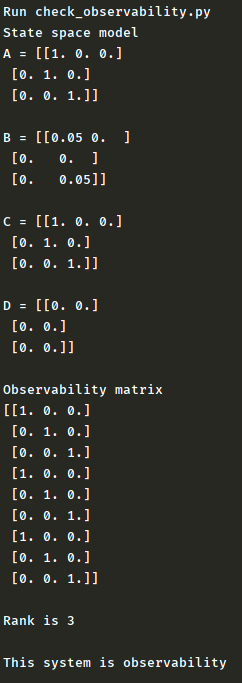
ここで計算される可観測性行列は、

となり、この行列のランクは3となる
ので、このシステムは可観測である
いう事になります。
GitHubリポジトリ
今回紹介したサンプルプログラムは、
こちらで公開しています。
可制御判定プログラム
github.com
可観測判定プログラム
github.com