詳解確率ロボティクス Pythonによる基礎アルゴリズムの実装 (KS理工学専門書)

はじめに

前回の記事では、複雑な形状の分布を持つデータを
分析し、確率分布にモデル化する方法と、そのための
Juliaサンプルコードについて紹介しました。

www.eureka-moments-blog.com

ここまでは主に1次元のデータを扱ってきましたが、
実際はロボットの姿勢である $[x, y, \theta$ ]といったように、
多次元のデータを扱う事も多々あります。

今回の記事では、2次元のガウス分布に従うデータを例に、
多次元データの処理方法と、Juliaサンプルコードについて
紹介します。

GitHubリポジトリ

本記事で紹介するコードは全てこちらのGitHubリポジトリで
公開しています。
github.com

サンプルデータの2次元ガウス分布

今回はサンプルデータとして、下記ディレクトリにある
データを取り上げます。
data/sensor_data_700.txt

これは、距離700[mm]先にある壁をLiDARと光センサで
観測したときのセンサ値です。このデータから特定の
条件を満たすデータを抽出して、2次元のヒストグラム
に可視化するのを次のコードで行います。
src/prob_stats/multi_dim_gauss_dist/marginal_kde/marginal_kde_700.jl

module MarginalKde700
    using DataFrames, CSV, StatsPlots
    pyplot()

    function main(is_test=false)
        # input
        data_path = joinpath(split(@__FILE__, "src")[1], "data/sensor_data_700.txt")
        df_org = CSV.read(data_path, DataFrame, 
                      header=["date", "time", "ir", "lidar"],
                      delim=' ')
        
        # extract between 12 and 16 o'clock
        df_ext = df_org[(df_org.time.>=120000).&(df_org.time.<160000),:]

        # plot marginal kde
        marginalkde(df_ext.ir, df_ext.lidar, c=:ice, 
                    xlabel="ir", ylabel="liDAR")

        if is_test == false
            save_path = joinpath(split(@__FILE__, "src")[1], "src/prob_stats/multi_dim_gauss_dist/marginal_kde/marginal_kde_700.png")
            savefig(save_path)
        end
    end
end

このコードでは、13行目で12時から16時のデータを抽出し、
そのうちのLiDARと光センサのセンサ値をカーネル密度推定で
確率密度関数を推定し、ガウス分布に当てはめることを
やっています。

カーネル密度推定についてはこちらの記事を参照ください。
ja.wikipedia.org

そしてコードを実行すると、次のグラフが作成されます。
f:id:sy4310:20210612124108p:plain

このヒストグラムは、両センサ値を変数としたときの
同時確率分布と解釈できます。

確率密度関数と共分散行列

今回のような多次元のガウス分布の確率密度関数は、
一般に次のように表されます。
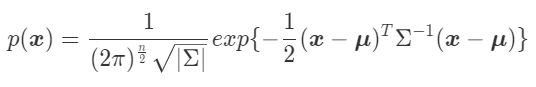
f:id:sy4310:20210612141732p:plain

式中の $\mu$ は平均値、 $\Sigma$ は共分散行列で、次のような
行列です。
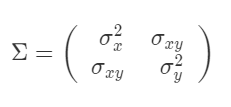
f:id:sy4310:20210612143027p:plain

$\sigma_x ^2$ , $\sigma_y ^2$ は $x$ と $y$ の分散、 $\sigma_{xy}$ は共分散です。
また、共分散行列の逆行列を $\Lambda$ とすると、
f:id:sy4310:20210612144010p:plain
となり、精度行列あるいは情報行列と呼ばれています。

共分散行列の計算

先程2次元のヒストグラムで可視化したデータの
共分散行列を計算してみましょう。次のコードを
実行することで、サンプルデータにおけるLiDARと
光センサのセンサ値の平均と分散、共分散を求める
ことができます。

src/prob_stats/multi_dim_gauss_dist/covariance/calc_covariance.jl

module CalcCovariance
    using DataFrames, CSV, Statistics

    function main()
        # input
        data_path = joinpath(split(@__FILE__, "src")[1], "data/sensor_data_700.txt")
        df_org = CSV.read(data_path, DataFrame, 
                      header=["date", "time", "ir", "lidar"],
                      delim=' ')
        
        # extract between 12 and 16 o'clock
        df_ext = df_org[(df_org.time.>=120000).&(df_org.time.<160000),:]

        # calculate
        println("Variance of ir: $(var(df_ext.ir))")
        println("Variance of lidar: $(var(df_ext.lidar))")
        
        diff_ir = df_ext.ir .- mean(df_ext.ir)
        diff_lidar = df_ext.lidar .- mean(df_ext.lidar)

        println("Mean of ir: $(mean(df_ext.ir))")
        println("Mean of lidar: $(mean(df_ext.lidar))")
        
        a = diff_ir .* diff_lidar
        println("Covariance: $(sum(a)/size(df_ext)[1])")
    end
end

15~16行目でそれぞれのデータの分散、
21~22行目でそれぞれの平均、そして
24~25行目で共分散を計算しており、
次のような結果となります。
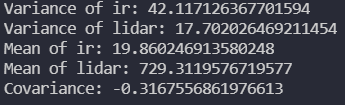
f:id:sy4310:20210612152010p:plain

以上より、次のような平均値と共分散行列が
得られました。
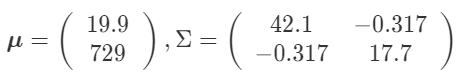
f:id:sy4310:20210612153251p:plain

これらを使い、最後に次のコードで
ガウス分布を描画してみます。
src/prob_stats/multi_dim_gauss_dist/contour_pdf/contour_pdf.jl

module ContourPdf
    using DataFrames, CSV, Statistics, LinearAlgebra
    using Base.Iterators, Plots
    pyplot()

    function pdf(x, mu, cov_mat)
        # determinant
        det_mat = det(cov_mat)

        diff_x = x - mu
        return exp(-((diff_x'/cov_mat)*diff_x)/2)/(2*pi*sqrt(det_mat))
    end

    function main(is_test=false)
        # input
        data_path = joinpath(split(@__FILE__, "src")[1], "data/sensor_data_700.txt")
        df_org = CSV.read(data_path, DataFrame, 
                      header=["date", "time", "ir", "lidar"],
                      delim=' ')
        
        # extract between 12 and 16 o'clock
        df_ext = df_org[(df_org.time.>=120000).&(df_org.time.<160000),:]

        # variance
        var_ir = var(df_ext.ir)
        var_lidar = var(df_ext.lidar)

        #covariance
        diff_ir = df_ext.ir .- mean(df_ext.ir)
        diff_lidar = df_ext.lidar .- mean(df_ext.lidar)
        a = diff_ir .* diff_lidar
        covar = cov(df_ext.ir, df_ext.lidar, corrected=false)
        
        # covariance matrix
        cov_mat = [var_ir covar; covar var_lidar]

        # mean(mu)
        mu = [mean(df_ext.ir); mean(df_ext.lidar)]

        # plot contour
        vx = 0:40
        vy = 710:750
        z = [pdf([x; y], mu, cov_mat) for x in vx, y in vy]
        contour(z', label="contour", c=:haline, xlabel="x", 
                ylabel="y", aspect_ratio=:equal)
        
        if is_test == false
            save_path = joinpath(split(@__FILE__, "src")[1], "src/prob_stats/multi_dim_gauss_dist/contour_pdf/contour_pdf.png")
            savefig(save_path)
        end
    end
end

まず、6~12行目で確率密度関数を定義しておきます。
データから求めた平均値と共分散行列、変数の各値を
入力として、確率密度を計算します。

そして、40~45行目で各X-Y座標における確率密度を
計算し、それを高さ情報とした等高線グラフを描画
します。

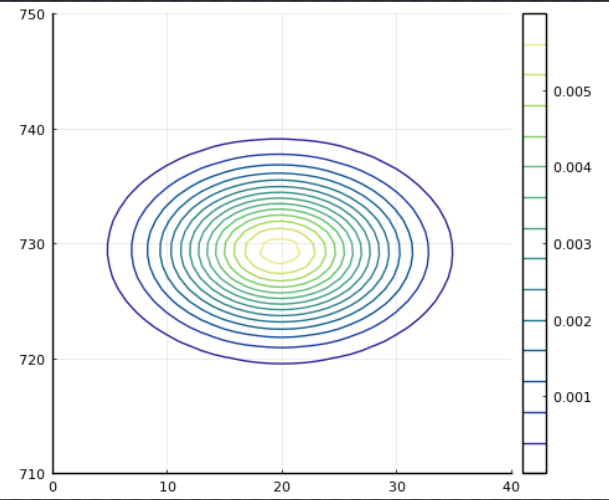
先に求めた平均値を中心に左右対称に広がり、
同じく先に示した2次元ヒストグラムとほぼ
同じ形状になっていることが分かります。
f:id:sy4310:20210612171300p:plain

共分散とは？

今回のような2次元データの場合、共分散は次の
式で求められます。
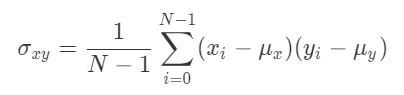
f:id:sy4310:20210612172825p:plain

これを見ると、求められる値は平均値に対して
$x_i$ , $y_i$ がともに大きいか小さいと正になり、
そうでなければ負となることが分かります。

先程のガウス分布の等高線を描画するコードで、
共分散行列を計算する部分を次のように変更
してみましょう。

# covariance matrix
cov_mat = [var_ir covar; covar var_lidar]
cov_mat[1, 2] += 20
cov_mat[2, 1] += 20

これにより、元々の共分散は負の値でしたが、
20が足されたことで正の値になり、ガウス分布の
等高線は次のように変わります。
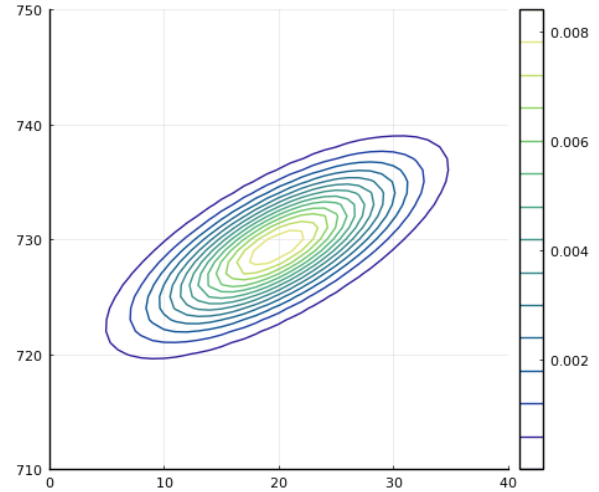
f:id:sy4310:20210612174157p:plain

このグラフから、一方のデータの値が大きくなる
あるいは小さくなると、もう一方も同様に変化する
という頻度が相対的に高いということが分かり、
共分散の値を見ることでも、なんとなくその傾向を
把握することができます。

誤差楕円

今度は、下記のコードにより形状が異なる三つの
ガウス分布を描画してみます。
src/prob_stats/multi_dim_gauss_dist/multiple_gauss_dist.jl

module MultiGaussDist
    using Plots, Base.Iterators, LinearAlgebra
    pyplot()
    
    function pdf(x, mu, cov_mat)
        # determinant
        det_mat = det(cov_mat)

        diff_x = x - mu
        return exp(-((diff_x'/cov_mat)*diff_x)/2)/(2*pi*sqrt(det_mat))
    end

    function main(is_test=false)
        # x-y grid
        vx = 0:200
        vy = 0:100

        # mu, covariance matrix
        # contour a
        mu_a = [50; 50]
        cov_a = [50 0; 0 100]
        # contour b
        mu_b = [100; 50]
        cov_b = [125 0; 0 25]
        # contour c
        mu_c = [150; 50]
        cov_c = [100 -25*sqrt(3); -25*sqrt(3) 50]

        # probability density
        # contour a
        z_a = [pdf([x; y], mu_a, cov_a) for x in vx, y in vy]
        # contour b
        z_b = [pdf([x; y], mu_b, cov_b) for x in vx, y in vy]
        # contour c
        z_c = [pdf([x; y], mu_c, cov_c) for x in vx, y in vy]

        # plot contours
        contour(vx, vy, z_a', c=:haline, aspect_ratio=:equal)
        contour!(vx, vy, z_b', c=:haline, aspect_ratio=:equal)
        contour!(vx, vy, z_c', c=:haline, aspect_ratio=:equal)
        
        if is_test == false
            save_path = joinpath(split(@__FILE__, "src")[1], "src/prob_stats/multi_dim_gauss_dist/multiple_gauss_dist/multiple_gauss_dist.png")
            savefig(save_path)
        end
    end
end

18~27行目で定義しているように、ここでは
下記三種類の平均値と共分散行列を持つ
ガウス分布としています。
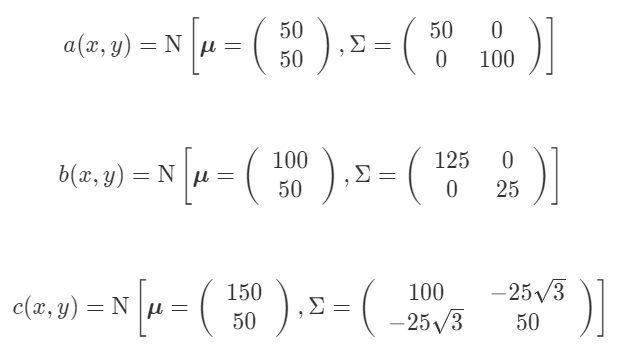
f:id:sy4310:20210612220908p:plain

そして先に紹介したコードを実行すると、
a, b, cそれぞれのガウス分布が左から順番に
並んだこちらのような図が描画されます。
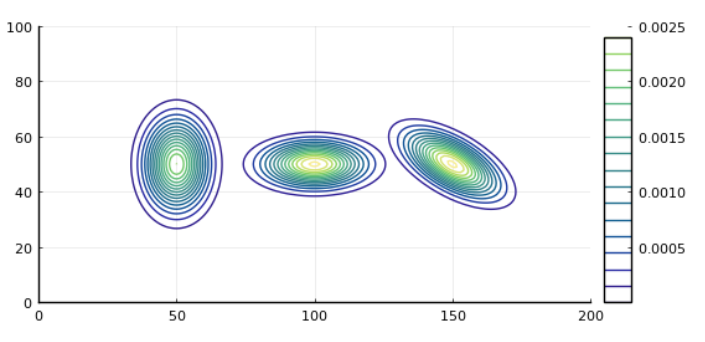
f:id:sy4310:20210612215658p:plain

それぞれに対応した平均値と共分散行列を
見てみると、分散 $\sigma_x ^2$ , $\sigma_y ^2$ の大きさが
それぞれの軸方向の分布の広がりを決め、
共分散 $\sigma_{xy} ^2$ が0でない正か負の値になると、
分布が傾きを持つ(回転する)ことが分かります。
またこのとき、分布は楕円形となります。

ここで、cの分布の共分散行列 $\Sigma$ の固有値と
固有ベクトルを計算し、分布の傾きを調べてみます。
固有値/固有ベクトルと楕円形の関係は、こちらの記事を
参照ください。

www.rikasuki.jp

次のコードを実行すると、cの分布の固有値/固有ベクトルを
計算し、分布の楕円の長軸方向と短軸方向のベクトルを一緒に
描画してくれます。
src/prob_stats/multi_dim_gauss_dist/eigen/calc_plot_eigen.jl

module CalcPlotEigen
    using Plots, Base.Iterators, LinearAlgebra
    pyplot()

    function pdf(x, mu, cov_mat)
        # determinant
        det_mat = det(cov_mat)

        diff_x = x - mu
        return exp(-((diff_x'/cov_mat)*diff_x)/2)/(2*pi*sqrt(det_mat))
    end

    function main(is_test=false)
        # x-y grid
        vx = 0:200
        vy = 0:100

        # mu, covariance matrix
        mu = [150; 50]
        cov = [100 -25*sqrt(3); -25*sqrt(3) 50]

        # calculate eigen values/vectors
        eig_vals, eig_vecs = eigen(cov)
        println("Eigen Values: $(eig_vals)")
        println("Eigen Vectors: $(eig_vecs)")
        println("Eigen Vector1: $(eig_vecs[:, 1])")
        println("Eigen Vector2: $(eig_vecs[:, 2])")

        # long or short
        if eig_vals[1] > eig_vals[2]
            long_val = eig_vals[1]
            long_vec = eig_vecs[:, 1]
            short_val = eig_vals[2]
            short_vec = eig_vecs[:, 2]
        else
            long_val = eig_vals[2]
            long_vec = eig_vecs[:, 2]
            short_val = eig_vals[1]
            short_vec = eig_vecs[:, 1]
        end
        println("Long Value: $(long_val)")
        println("Long Vector: $(long_vec)")
        println("Short Value: $(short_val)")
        println("Short Vector: $(short_vec)")

        # plot
        z = [pdf([x; y], mu, cov) for x in vx, y in vy]
        contour(vx, vy, z', c=:haline, aspect_ratio=:equal)
        long = 2 * sqrt(long_val) * long_vec
        short = 2 * sqrt(short_val) * short_vec
        quiver!([mu[1]], [mu[2]], quiver=([long[1]], [long[2]]), 
                c=:red, aspect_ratio=:equal)
        quiver!([mu[1]], [mu[2]], quiver=([short[1]], [short[2]]), 
                c=:blue, aspect_ratio=:equal)
        
        if is_test == false
            save_path = joinpath(split(@__FILE__, "src")[1], "src/prob_stats/multi_dim_gauss_dist/eigen/contour_eigen.png")
            savefig(save_path)
        end
    end
end

23行目で固有値/固有ベクトルが計算されますが、
長軸方向と短軸方向のどちらかに対応した2つの
値とベクトルが得られます。そのため、30~40行目で
どちらが長軸か短軸かを判定する必要があります。
そして、計算結果はこちらのようになります。
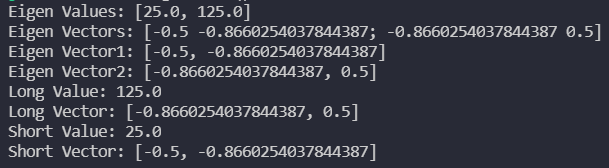
f:id:sy4310:20210613002456p:plain

長軸方向の固有値が $l_1$ , 短軸方向の固有値が $l_2$ とすると、
$l_1=125, l_2=25$ 、そしてそれぞれに対応する固有ベクトルは
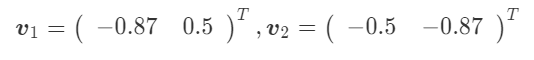
f:id:sy4310:20210613114028p:plain
となります。

このとき、元の共分散行列 $\Sigma$ と固有値/固有ベクトルの間には
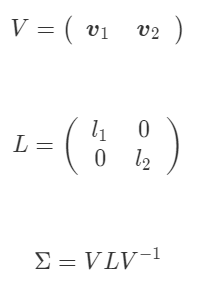
f:id:sy4310:20210613121505p:plain
という関係が成り立ちます。
$L$ は対角線上の要素以外がゼロの対角行列、
$V$ は固有ベクトルを２つ並べた2×2の行列
となります。

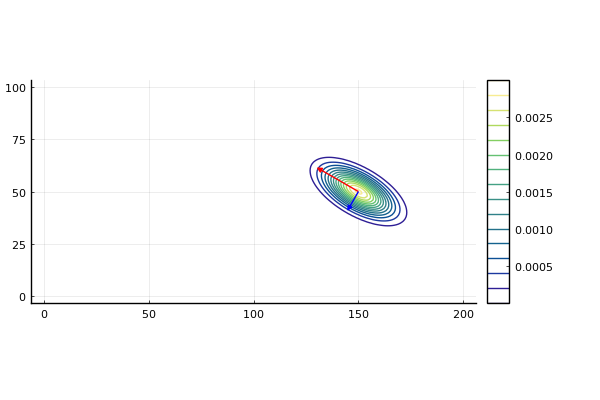
最後にこれらの計算結果を使って、コードの49~50行目で
長軸方向と短軸方向を向き、それぞれの長さの比に比例した
ベクトル $\sqrt{l_1}v_1, \sqrt{l_2}v_2$ を求めて、51~54行目で
ガウス分布に重ねて次のように描画します。
f:id:sy4310:20210613114754p:plain