EurekaMoments

ロボットや自動車の自律移動に関する知識や技術、プログラミング、ソフトウェア開発について勉強したことをメモするブログ

書籍「SLAM入門」の読書録～センサフュージョンとループ閉じ込み～

Robotics SLAM C++

SLAM入門: ロボットの自己位置推定と地図構築の技術

SLAM入門: ロボットの自己位置推定と地図構築の技術

作者:友納正裕
発売日: 2018/03/03
メディア: 単行本（ソフトカバー）

目次

目次
目的
SLAMにおける退化とは
退化を防ぐためのセンサフュージョン
ループ閉じ込みとは
ソフト設計
GitHub

目的

書籍「SLAM入門」を参考に、SLAMでロボット位置を推定する際のセンサフュージョンとループ閉じ込みについて理解する。
サンプルコードを参考に、C++での設計思想について理解する。

SLAMにおける退化とは

一般的には、計測されたスキャンデータにランドマークが多く含まれているほど、安定して解が求まりやすくなる。
ただし、スキャンされた周囲の環境があまり特徴的でなく、スキャンマッチングがどこの位置でも合うようになってしまい、ロボット位置が一意に定まらなくなる。
このように、ロボット位置を一意に定めるために必要な情報が不足した状態になる状況を退化と呼ぶ。

f:id:sy4310:20200726213441p:plain

退化を防ぐためのセンサフュージョン

複数のセンサから得られたデータを統合してロボットの状態推定を行う技術をセンサフュージョンという。
これによってロボット位置推定に必要な情報の不足を補い、SLAMの退化を防ぐ事が可能になる。
複数のセンサを用いるため、同時に複数パターンのロボット推定位置が求められる。
各センサデータの信頼性に基づいて、ロボット推定位置の重み付き平均を計算する。

f:id:sy4310:20200730215511p:plain

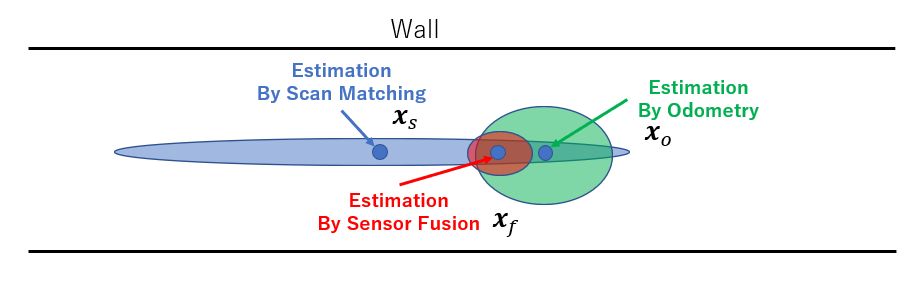
オドメトリによる位置を $x_o$ 、スキャンマッチングによる位置を $x_s$ 、また、それぞれの重みを $W_o$ , $W_s$ とする。
これらの重み付き平均でセンサフュージョンによるロボット位置 $x_f$ を求めると下記のようになる。

f:id:sy4310:20200730222200p:plain

この重みパラメータは、推定されるロボット位置誤差の共分散より決定されるのが一般的である。
$x_o$ の誤差分散を ${\sigma_o}^2$ 、 $x_s$ の誤差分散を ${\sigma_s}^2$ 、 $x_f$ の誤差分散を ${\sigma_f}^2$ とする。
この時の重み $W_o$ , $W_s$ は、求めたい位置 $x_f$ の誤差分散である ${\sigma_f}^2$ が最小となるように決めると考える。
分散 ${\sigma_f}^2$ は下記の計算式で求められる。

f:id:sy4310:20200731221358p:plain

これが最小とする $W_o$ , $W_s$ は下記のように求められる。

f:id:sy4310:20200731224728p:plain

以上より、求めたい位置 $x_f$ と、その誤差分散 ${\sigma_f}^2$ は下記のように求められる。

f:id:sy4310:20200801005239p:plain

ループ閉じ込みとは

ここで言うループとは、以前通った場所を再び通る経路である。
SLAMではランドマーク位置を推定し、それに基づいて自己位置推定もするため、それによる累積誤差でループは閉じない事が多い。
ループが閉じない事で地図が歪み、ロボットが障害物に衝突したり、目的地までの経路がおかしくなってしまう。

f:id:sy4310:20200728211830p:plain

ロボットが再び同じ場所を通った事を検出し、そのループが閉じた位置を正しく求める必要がある。(ループ検出)
求めた位置でループを閉じると、それまでに構築してきた地図上のランドマークや、ロボットの移動軌跡との辻褄が合わなくなる。
そのため、ループ検出位置から過去を遡る形でロボットの移動軌跡と地図を修正する処理が後工程として必要になる。(ポーズ調整)

f:id:sy4310:20200729201431p:plain

ソフト設計

センサフュージョン

クラス

PoseFuser
スキャンマッチングで求めた位置の共分散、オドメトリで求めた位置の共分散をメンバ変数に持つ。
スキャンマッチング時の対応付けや、共分散の計算自体は、それらを担うクラスのインスタンスをメンバに持つ事で実行する。

f:id:sy4310:20200801134501p:plain

メソッド

共分散による重み付き平均の計算

fusePose()
スキャンマッチングとオドメトリの共分散は、CovarianceCalculatorクラスのメソッドを呼び出す事で計算する。
fuseメソッドを呼び出して、それぞれの推定位置と共分散を融合させる。

f:id:sy4310:20200801135402p:plain

位置と共分散の融合

fuse()
それぞれの共分散は正規分布に従うと仮定して融合する。
方位角は-180°~180°に正規化されているが、このままでは境界付近で値が飛び、後の処理が破綻する可能性がある。
スキャンマッチングとオドメトリの方位角の差をとり、それが-180°~180°の範囲を超える場合は、スキャンマッチングの方位角に360°を加算あるいは減算して値の飛びを防ぐ。

f:id:sy4310:20200801144111p:plain

共分散の計算

クラス

CovarianceCalculator
スキャンマッチングとオドメトリのそれぞれの誤差共分散を計算する。

f:id:sy4310:20200801144523p:plain

メソッド

スキャンマッチングの共分散の計算

calIcpCovariance()

f:id:sy4310:20200801151429p:plain

計算した共分散行列を関数calEigen()で固有値分解し、退化具合をチェックできる。

f:id:sy4310:20200801152212p:plain

2つの固有値の比が大きい場合、ある軸の不確実性は大きく、もう一方の軸の不確実性は小さいという事になる。
廊下のような環境における退化の指標になる。

f:id:sy4310:20200801152605p:plain

kriver-1.hatenablog.com

convexbrain.github.io

オドメトリの共分散の計算

calMotionCovarianceSimple()
共分散行列は対角成分のみを計算する。
対角成分は、位置座標x, yと方位角の分散。それぞれに相関はない独立な状態と仮定すると、他の共分散成分は0と考える事が出来る。

f:id:sy4310:20200801152720p:plain

ループ検出

クラス

LoopDetector
現在位置と再訪点の距離閾値を4mに設定。この範囲内で最短距離にある点を再訪点とする。
累積走行距離の差の閾値を10mに設定。これが現在位置と近すぎる場合は探索対象から外す。

f:id:sy4310:20200801163136p:plain

メソッド

現在位置と近く、現在スキャンに形状が合う場所を検出する

detectLoop()
現在位置に最も近い部分地図と再訪点候補を求める。
最も近い部分地図を参照スキャンとし、現在スキャンと形状が一致するところを再訪点として決定。

f:id:sy4310:20200801163752p:plain

再訪点位置の計算

estimateRevisitPose()
最も近い部分地図の中から、現在スキャンと参照スキャンが最も合うところをICPで求める。
点の対応率0.9以上、マッチング点数が50点以上なら最適とする。

f:id:sy4310:20200801164323p:plain

GitHub

記載されているUMLのダイアグラムは、全て下記のGitHubリポジトリで公開済み。