Juliaで学ぶ確率ロボティクス～センサ値の度数分布～

詳解 確率ロボティクス Pythonによる基礎アルゴリズムの実装 (KS理工学専門書)

目次

はじめに

前回の記事では、センサデータの値をざっくり
解析して概要を出力するJuliaコードについて
紹介しました。

www.eureka-moments-blog.com

それに引き続き今回は、センサ値をヒストグラムで
可視化し、そこから平均や標準偏差、分散を計算
するJuliaサンプルコードを紹介します。

GitHubリポジトリ

本記事で紹介するJuliaコードは全てこちらの
リポジトリにて公開しています。
github.com

ヒストグラムを描画するJuliaコード

まずはこちらのコードを使って、センサ値の
ヒストグラムを描画させます。
src/prob_stats/freq_dist/draw_histogram.jl

module DrawHistogram
    using Plots, DataFrames, CSV
    pyplot()

    function main()
        data_path = joinpath(split(@__FILE__, "src")[1], "data/sensor_data_200.txt")
        df_200_mm = CSV.read(data_path, DataFrame, 
                             header=["date", "time", "ir", "lidar"],
                             delim=' ')
        
        bin_min_max = maximum(df_200_mm.lidar) - minimum(df_200_mm.lidar)
        histogram(df_200_mm.lidar, bins=bin_min_max, label="histogram")

        save_path = joinpath(split(@__FILE__, "src")[1], "img/histogram_200_mm.png")
        savefig(save_path)

        return true
    end
end

描画させるデータは、壁までの距離を200mmに
設定してLiDARで計測した値です。
data/sensor_data_200.txt

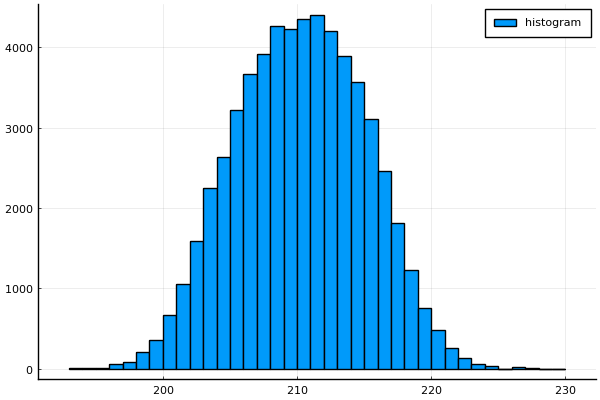
そして、上記のコードを実行すると下記のような
ヒストグラムが描画されます。

コードの内容について説明すると、
最初に必要なパッケージを取り込みます。

using Plots, DataFrames, CSV
pyplot()

ここで初めて、描画用パッケージであるPlotsが
登場します。Plotsはこちらの記事にあるように
好みに合わせて様々なバックエンドを設定する
ことができます。
自分の場合は、見た目が綺麗になるとされている
pyplotを設定しています。
qiita.com

次のコードでは、サンプルデータのファイルを
読み込み、各データ列にカラム名を割り当てた
データフレームを作成しています。

data_path = joinpath(split(@__FILE__, "src")[1], "data/sensor_data_200.txt")
df_200_mm = CSV.read(data_path, DataFrame, 
                     header=["date", "time", "ir", "lidar"],
                     delim=' ')

そして、作成したデータフレームから
lidarのデータ列を取り出し、下記の
コードでヒストグラムを描画します。

bin_min_max = maximum(df_200_mm.lidar) - minimum(df_200_mm.lidar)
histogram(df_200_mm.lidar, bins=bin_min_max, label="histogram")

histogram関数を使って描画するのですが、
引数binsで横軸の区間の数を指定できます。
ここでは、区間の幅を1にするために、
センサ値の最大値と最小値の差を区間の
数に指定しています。

頻度、ノイズ、バイアス

上記のヒストグラムを見ることで、

• 観測範囲は194[mm]から226[mm]まで
• 210[mm]付近が高頻度
• 左右に離れるほど頻度が低くなる

といったことが分かります。
このセンサ値の真値は200[mm]ですが、
実際にはある範囲内で変動(ノイズ)したり、
常に一定のずれ(バイアス)が生じる場合が
ほとんどです。

平均値

ここからはノイズの傾向を把握してみます。
まず最初に、センサ値の平均値を計算し、
その次に、ばらつきの程度を表す分散や
標準偏差を求めます。

このとき、センサ値のリストを下記のように
数式化すると、

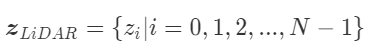
これらの平均値は下記の式で計算されます。

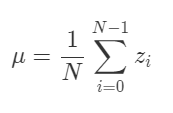
Juliaのコードでは次のように計算できます。

a = sum(df_200_mm.lidar)
println("Sum of sensor data = $a")
b = length(df_200_mm.lidar)
println("Length of sensor data = $b")
mean_1 = a / b
mean_2 = mean(df_200_mm.lidar)
println("Mean(Sum / Length) = $mean_1")
println("Mean(mean()) = $mean_2")

1行目から5行目はN数と合計から普通に
計算するやり方、6行目は各種統計値の
計算をするためのパッケージである
Statisticsに含まれるmean関数で求める
方法です。

このコードの実行結果は次のようになり、
当然ながら両者のやり方による計算結果は
一致します。

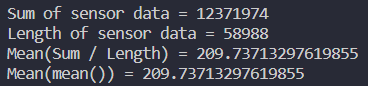
続いてこちらのコードで、計算した平均値
をヒストグラムに書き込んでみます。

bin_min_max = maximum(df_200_mm.lidar) - minimum(df_200_mm.lidar)
histogram(df_200_mm.lidar, bins=bin_min_max, color=:orange, label="histogram")
plot!([mean_1], st=:vline, color=:red, ylim=(0, 5000), linewidth=5, label="mean")

1行目と2行目は既に紹介したヒストグラム
描画用のコードと同じです。これらに
加えて、平均値のところに赤い垂直線を
引くコードを追加しています。
3行目のplot!関数により、先に描画された
ヒストグラムに別のグラフを上書きする
ことができます。その際のグラフの種類は
引数stで指定し、今回は垂直線であるvlineと
しています。

これにより、ヒストグラムの頂上付近に
平均値があることが分かります。

分散

次に分散を求めます。

分散には下記のような標本分散と、

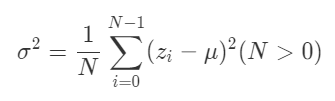
下記のような不偏分散があります。

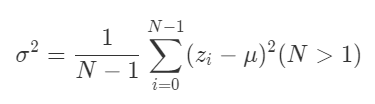
両者の違いについては、こちらの記事の
説明が分かりやすいので参照ください。
ai-trend.jp

そして、上記の計算を次のような
Juliaコードで実行できます。

zs = df_200_mm.lidar # observation
mean_def = sum(zs) / length(zs) # mean
diff_square = [(z - mean_def)^2 for z in zs]
        
sampling_var = sum(diff_square) / length(zs) # sampling variance
unbiased_var = sum(diff_square) / (length(zs) - 1) # unbiased variance

println("Sampling Variance = $sampling_var")
println("Unbiased Variance = $unbiased_var")

このコードでは、標本分散(Sampling
variance)と不偏分散(Unbiased variance)
をセンサ値の平均(2行目)と各値と平均値の
差の2乗(3行目)から計算しています。

また、Statisticsパッケージにあるvar関数を
使って同様の計算をすることもできます。
var関数の引数correctedをfalseにすると
標本分散、trueにすると不偏分散を出力する
ようになります。

stats_sampling_var = Statistics.var(zs, corrected=false)
stats_unbiased_var = Statistics.var(zs, corrected=true)

println("Sampling Variance by Statistics = $stats_sampling_var")
println("Unbiased Variance by Statistics = $stats_unbiased_var")

上記の2つのコードの実行結果は次のように
なり、当然ですが両者の結果は同じになります。

標準偏差

最後に標準偏差を計算するコードについて
紹介します。標準偏差は分散の正の平方根
なので、1行目と2行目のようにsqrt関数に
既に求めた分散を入力して計算することが
できます。
また、Statisticsパッケージのstd関数を
使って同様の計算が出来ます(3行目)

sampling_std_dev = sqrt(sampling_var)
unbiased_std_dev = sqrt(unbiased_var)
stats_std_dev = Statistics.std(zs, corrected=false)

println("Sampling standard deviation = $sampling_std_dev")
println("Unbiased standard deviation = $unbiased_std_dev")
println("Standard deviation by Statistics = $stats_std_dev")

これらのコードの計算結果は次の
ようになります。

まとめ

センサ値の度数分布として、
ヒストグラムの描画、
平均値、分散、標準偏差を
計算するJuliaコードを紹介
しました。
次回は、センサ値の確率分布を
計算するJuliaコードについて
紹介します。