機械学習に必要な数学の基本についての勉強メモ: ベクトルと微分編

Pythonで動かして学ぶ！ あたらしい機械学習の教科書

目次

はじめに

機械学習、深層学習を学ぶ上で、数学の知識は絶対に必要だと思います。自分も最近になって機械学習、深層学習について本格的に勉強を開始しましたが、まず最初に感じたのは数学の基本をいろいろと忘れているな、という事です。そんな時に上記の技術書を見つけたので、これを利用してPythonでのプログラミングを交えながら数学の基本について学び直し、その中から重要だと思った部分やサンプルコードをこの記事にメモしていこうと思います。

Pythonで縦ベクトルを表す

numpyのndarray型は、１次元では縦と横の区別がなく常に横ベクトルとして扱われる。しかし、特別な形の２次元のndarrayとして縦ベクトルを表すことができる。

# 2 X 2
np.array([[1, 2], [3, 4]])

# output
[[1 2]
 [3 4]]

この方式で2X1の２次元配列を作れば縦ベクトルを表す事が出来る。

# 2 X 1
np.array([[1], [2]])

# output
[[1]
 [2]]

ベクトルの足し算、引き算の図形的な解釈

ベクトルは図形的に解釈できる。要素を座標点とし、原点からその座標点に向かう矢印と考える。2つのベクトルa, bがあるとすると、ベクトルの足し算はaとbを隣り合う辺とした平行四辺形の対角線を求める演算と解釈できる。


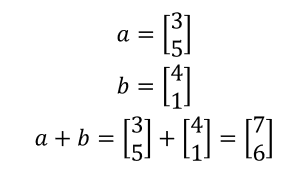
引き算の場合、a - bはa + (-b)として、aと-bと足し算とみなせる。-bはbと反対方向を向いた矢印であり、aと-bを隣り合う2辺とした平行四辺形の対角線となる。

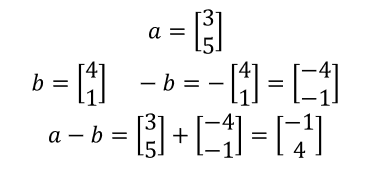
ベクトルの内積

内積は、同じ次元を持つ2つのベクトル同士の演算であり、"・"で表す。対応する要素同士を掛け算し、その和をとる。
Pythonでは以下のように書いて内積を計算する。

b = np.array([1, 3])

c = np.array([4, 2])

b.dot(c)

# output
10

内積を図形的に表すと以下のように、bをcに射影したベクトルをb'とし、b'とcの長さを掛け合わせたものとなる。

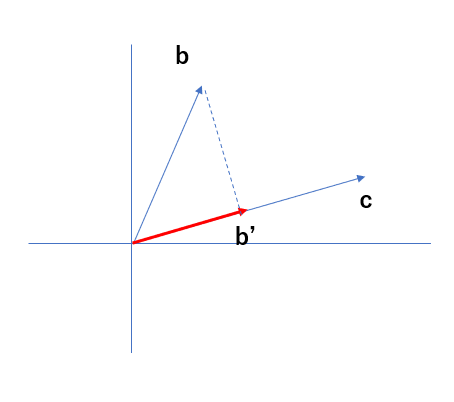
内積が大きな値をとるのは、２つのベクトルが似たような方向を向いているときである。逆に、小さな値をとるときは、２つのベクトルが垂直に近いときである。以上のことから、内積とは２つのベクトルの類似度に関係しているということになる。

Pythonでのベクトルの大きさの計算

a = np.array([1, 3])
np.linalg.norm(a)

# output
3.16227766017

ベクトルの内積を和の記号を使って表す

以下の式の左は行列表記(ベクトル表記)、右は成分表記と呼ぶ。
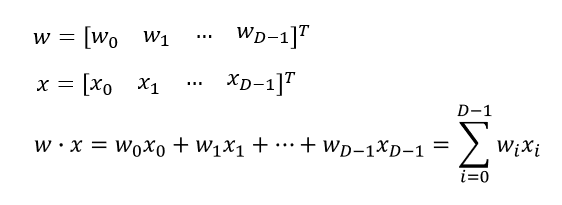
また、和を内積として計算することもできる。

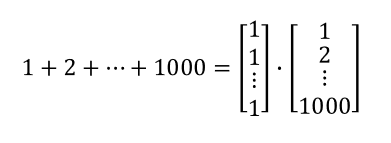
こうすることで、Pythonではfor文を使った和の計算を内積で計算することができる。この方が計算処理を高速にできる。

import numpy as np
a = np.ones(1000)      # [1 1 1 ... 1]
b = np.arange(1, 1001) # [1 2 3 ... 1000]
a.dot(b)

# output
500500.0

積の記号

f(n)のnを、aから1ずつ増やしbになるまで変化させ、すべてのf(n)を掛け算する。

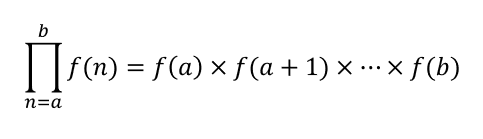
機械学習における微分の在り方

機械学習の問題は、大抵の場合、ある関数が最小(または最大)をとる入力を探す問題(最適化問題)に帰着される。関数の最小地点は、傾きが0になるという性質があることから、このような問題を解くには、関数の傾きを知ることが重要となる。その傾きを導出する方法が微分である。

入れ子の関数の微分

機械学習では、入れ子の関数の微分が欲しいことが多々ある。入れ子の関数とは、例えば以下の式のような関数である。

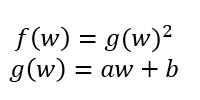
単純には、g(w)を上の式に代入して展開すれば、微分を計算することができる。

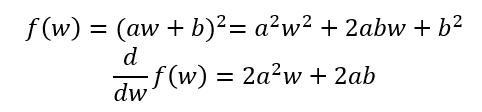
しかし、式が複雑で展開するのが大変な場合もある。そういうときは、連鎖律と呼ばれる以下の公式が役に立つ。

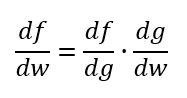
これを先程の式に適用すると、

となって結果としては同じ式が得られる。また、この連鎖律は、三重にも四重にも拡張することが可能である。例えば以下のような場合である。

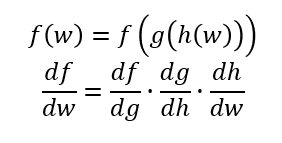
機械学習における偏微分の在り方

機械学習で実際に出てくるのは純粋な微分ではないことが多い。それは以下のように複数の変数を持つ関数であり、そのうち一つの変数だけに着目して、他の変数を定数とみなして微分するものである。これを偏微分という。

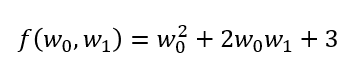
この関数でw0を定数とすると、これは変数w1の１次関数となり、w1を定数とすると変数w0の２次関数となる。以上のことから、この関数は見る方向によって形状が異なる３次元的に歪みを持ったグラフを表しているということになる。
そして、この関数をw0で偏微分するということは３次元グラフをw0の軸に平行な方向から２次元グラフとして見ることであり、w1の値を定数とすることで断面が決まる。例として、w1を1, -1としてw0で偏微分したグラフは以下のようになる。

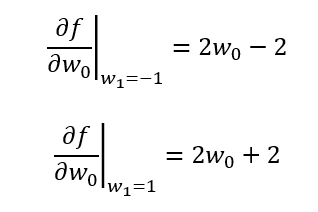
同様にw0を1, -1としてw1で偏微分したグラフは、

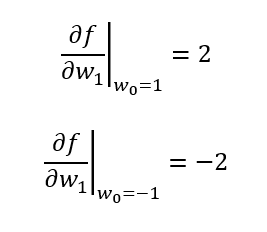
となる。微分とは関数の傾きを知ることなので、w1で指定した断面で切ったグラフの傾き、また、w0で指定した断面で切ったグラフの傾きを偏微分により求めることができるということになる。

傾きをベクトルとして解釈する

前述した２つの傾きをセットにしてベクトルとして解釈することができる。これを、関数fのwに関する勾配(勾配ベクトル, gradient)と呼び、次式のように表す。

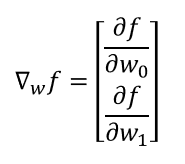
勾配は、傾きの最も大きい方向とその大きさを表す。

勾配を図で表す

前述したw0とw1に関する関数を等高線で表し、wの空間を格子状に区切ったときの各点における勾配ベクトルを矢印で表すと下記の図のようになる。

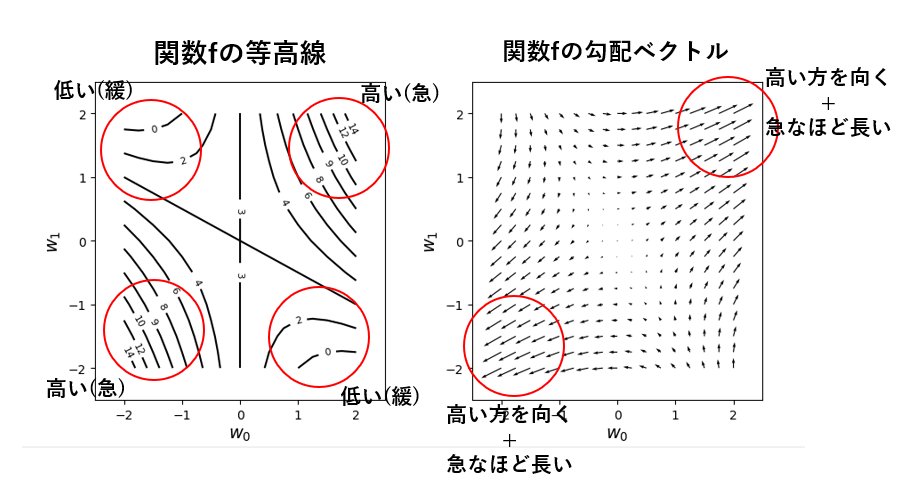
左の図の等高線プロットの数値を見ると、右上と左下が高くて、左上と右下が低い形状をしていることが分かる。そして、この勾配ベクトルを表したのが右の図である。各地点におけるベクトルは、傾斜が高い方を向いており、傾斜が急なほど長くなっていることが分かる。
ベクトルの方向に辿ればグラフのより高い方に進み、逆を辿ればグラフのより低い方へ進める。以上のことから、勾配とは関数の最大 or 最小点を探索するのに重要な概念である。そして機械学習では、誤差関数の最小点を求めるために誤差関数の勾配を計算する。
上記の図を表示するサンプルコードは以下のGitHubリポジトリで公開しています。

github.com

多変数の入れ子関数の微分

多層のニューラルネットワークの学習則を導出する際には、多変量の関数が入れ子になっている場合がある。例えば、g0とg1がw0とw1の関数で、fがg0とg1の関数となっている場合、fのw0に関する微分、w1に関する微分は連鎖律を使って以下のように表すことができる。

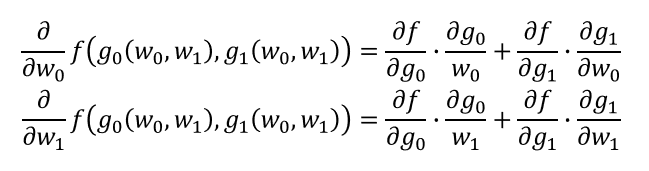
また、内部の関数が３個以上だったら、

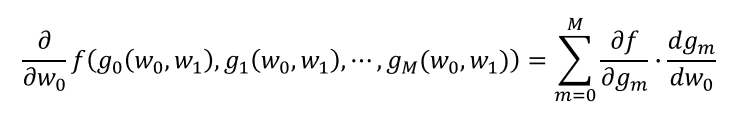
実際にニューラルネットワークの学習則を導出する場合は、このように２つ以上の関数の入れ子となる。

和と微分の交換

機械学習では、計算の過程で和の記号で表された関数を微分する機会が多々ある。例えば、以下のような式がある場合、ストレートに考えるなら、和を計算してから微分すればよいはずである。

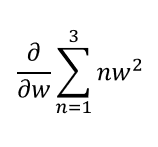
しかし、実際は各項の微分を計算してから、最後に和をとった場合でも答えは変わらない。

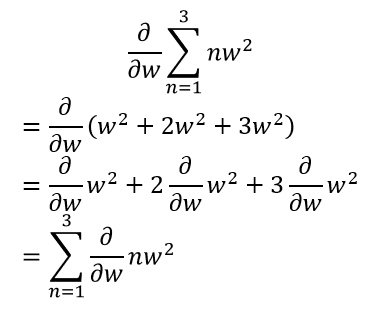
以上のことを踏まえて一般的な書き方をすれば、以下のようになり、微分の記号は和の記号の内側に入れて先に微分を計算することができると分かる。

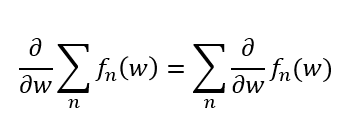
微分を先に計算してしまう方が計算が楽になったり、微分だけしか計算できないことが多々あるので、機械学習ではこの公式が多用される。