
- 作者:友納 正裕
- 発売日: 2018/03/03
- メディア: 単行本(ソフトカバー)
目次
目的
- 書籍「SLAMA入門」を参考に、SLAMでスキャンマッチングをする際のロボット位置推定について理解する。
- サンプルコードを参考に、C++での設計思想について理解する。
ICPの概要
- Iterative Closest Points
- 現在時刻のスキャンと過去の参照スキャンとの間で、各スキャン点の対応付けとロボットの位置推定を交互に繰り返す。
- 現在スキャンと参照スキャン間の誤差が最も小さいところが、尤もらしいロボットの位置だと判定する。
- 参照スキャンについては、こちらの記事を参照。
- 繰り返し回数を
、時刻
における
回目で求まるロボット位置を
とした場合、ICPの挙動は下記のようになる。
- ロボット位置の初期値は、オドメトリで予測した現在時刻のロボット位置を初期値にした方が良い結果を得られやすい。

スキャンデータ対応付けの概要
- 地図座標系における各スキャン点を
とし、下記の式で計算する。
- 座標変換のための回転行列を
, 並進ベクトルを
とする。

- 現在スキャン点
からのユークリッド距離が最も小さくなる参照スキャン点を
とする。

格子テーブル構造の概要
- 地図を格子状に区分けしてセルにスキャン点をセットしていく。
- 各セルに複数のスキャン点がある場合は、その点群の重心位置を求めてセルの代表点とする。

- 地図座標系での位置が求められたスキャン点と対応するセルのインデックス
,
を下記の式で求める。
: セルの1辺の長さ
: 小数点以下の切り捨て
,
: 地図範囲の下限値

- 現在スキャン点の最近傍点を探索する際は、現在スキャン点を中心にした円内にある参照スキャン点のみに対してユークリッド距離を計算する。
- 全ての参照スキャン点に対して線形探索する必要がないので効率的になる。

- kd木やR木のような空間検索手法を用いれば、さらに効率的な対応付けが可能となる。
ロボット位置推定の概要
- スキャンデータの対応付けに従い、下記の式により各点間の距離の二乗平均を求める。
- これをコスト関数とし、
が最小となる
を求める。
- 繰り返し回数が
回目の
と、
回目の
の差が閾値以下になれば計算を終了する。

- これは非線形最適化問題であり、最急降下法、ガウス-ニュートン法、レーベンバーグ-マーカート法、準ニュートン法、共役勾配法などがあり、これらの選び方によっても性能が変わる。
- 本書籍のサンプルプログラムでは、最もシンプルな再急降下法がデフォルトで用いられている。
位置最適化の概要
- 現在スキャン点と参照スキャン点の間のユークリッド距離よりも、参照スキャン点の接線までの垂直距離を用いてコスト関数を定義する方が、よりマッチング精度が高くなる場合がある。
- 垂直距離はスキャン点計測時の前処理で計算される法線ベクトルを利用して計算される。
- ユークリッド距離では、相反する方向の2点と対応付けられる事で、中途半端な状態に最適化されてしまう事がある。
- 垂直距離なら、対応点が完全に一致しなくても、正しいマッチングが得られやすくなる。

- デフォルトの最急降下法では、収束の速さはステップ幅に大きく依存する。
- 最適なステップ幅は動的に変わり得る。
- ブレント法による直線探索でステップ幅を動的に決めながら最急降下法を行う。
- C++では、Boostというライブラリを使う事で実装できる。
ソフト設計
データ対応付け
基底クラス
- 対応が取れた現在/参照スキャン点群を持つためのメンバ変数を定義する。
- setRefBase()で参照スキャン点群を格納。仮想関数にして、派生クラス側で実体を定義する。
- findCorrespondence()で各現在スキャン点と各参照スキャン点のペアを決めていく。

派生クラス: DataAssociatorLS

- 対応点を単純に線形探索で見つける。
- 現在スキャン点に対して、ユークリッド距離が閾値以下かつ最短距離にある参照スキャン点を対応付ける。

- 参照スキャン点群はvector型で保持する。

派生クラス: DataAssociatorGT
- 単純な線形探索では、スキャン点数が多くなるほど処理速度が遅くなる。
- 格子テーブル構造で参照スキャン点を管理する事で効率化を図る。

- 格子テーブル構造は、セル構造体のvector型で定義する。
- セルの構造体は、スキャン点群のvectorで定義する。
- セルサイズは0.05m、テーブルの1辺の半分を40mとする。

- addPoint()で参照スキャン点を格子テーブルに登録する。
- テーブルの領域内に入る点かどうかを最初にチェックする。

- makeCellPoints()で各セル内にあるスキャン点群の代表点を求める。
- 中にある点数が閾値以上のセルのみ処理する。
- 点群の重心点位置と法線ベクトルの平均を求めて、地図ベクトルに追加していく。
- 地図上の点数を減らしてメモリを節約する事が出来る。

- findClosestPoint()で現在スキャン点に最も近い参照スキャン点を格子テーブルから探す。
- スキャン点はロボット座標系なので、同時刻のロボット予測位置を使って地図座標系に変換する。
- 現在スキャン点の格子テーブル上のインデックスを見つけ、そこを中心に半径閾値の円を作る。
- 円内にあるセルにアクセスし、そのセル内にある参照点から閾値以内かつ最近傍の点を返す。

ロボット位置推定
コスト関数
- 基底クラスとして、CostFunctionクラスを定義。
- 対応付けた現在/参照スキャン点群をメンバ変数として持つ。
- 仮想関数としてcalValue()を宣言しておき、派生クラスの方で実体を定義させる。

- 派生クラス: CostFunctionED
- 2点間のユークリッド距離を用いたコスト関数を定義する。
- ユークリッド距離の2乗の総和を求めて、その平均値を評価値とする。
- 評価値は小さくなりすぎないように100倍する。
- 各点間のユークリッド距離が閾値以下の点数をカウントし、その比率を求めておく。

- 派生クラス: CostFunctionPD
- 2点間の垂直距離を用いたコスト関数を定義する。
- 垂直距離を用いる事以外はCostFunctionEDと同じ。

最適化
- 基底クラスとして、PoseOptimizerクラスを定義。
- 仮想関数でoptimizePose()を宣言し、派生クラスの方で実体を定義させる。

- 派生クラス: PoseOptimizerSD
- 最急降下法でコスト関数を最小化する。
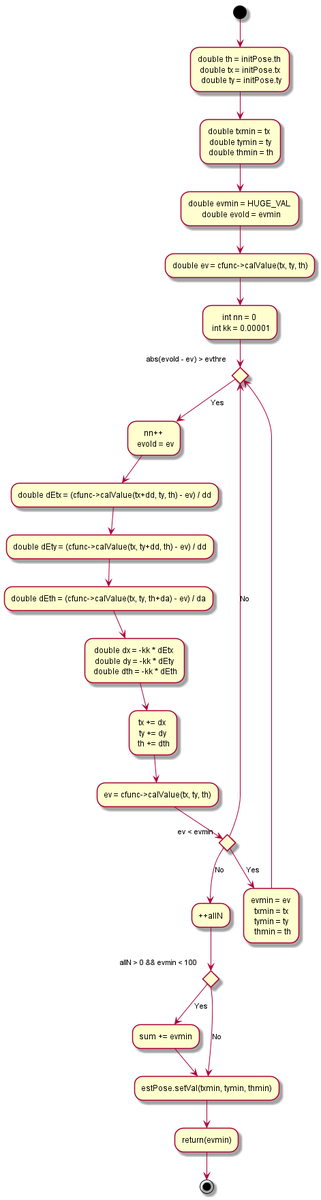
- 派生クラス: PoseOptimizerSL
- 最急降下法 + 直線探索でコスト関数を最小化する。

- boostライブラリのブレント法で直線探索を行うメソッド: search()
- 勾配方向にどれだけ進めばよいか、最適なステップ幅を見つける。

- 直線探索の目的関数: objFunc()

ロボット位置推定
- PoseEstimatorICPクラス
- ICPによりロボットの位置を推定する。
- ICPに使われたスキャン点数をメンバ変数に格納し、ループ検出時に活用する。

- 初期値を与えてロボットの推定位置を求めるメソッド: estimatePose()

GitHub
記載されているUMLのダイアグラムは、全て下記のGitHubで公開済み。