Table of Contents
- Table of Contents
- Introduction
- Author
- GitHub
- Input sample data: Weight of insect
- Target sample data: Sex of insect
- Sample data generation
- Policy to solve problem
- Classification with probability
- Maximum likelihood estimation
- Logistic Regression
- Cross entropy error
- Calculating parameter by Gradient method
- Summary of classification sequence
Introduction
This is my studying log about machine learning, supervised classification. I referred to a following book.

Pythonで動かして学ぶ!あたらしい機械学習の教科書 第2版 (AI & TECHNOLOGY)
- 作者: 伊藤真
- 出版社/メーカー: 翔泳社
- 発売日: 2019/07/18
- メディア: 単行本(ソフトカバー)
- この商品を含むブログを見る
I extracted some important points and some related sample python codes and wrote them as memo. In particular, this article focuses on 2 class classification with 1 dimensional input.
Author
GitHub
Sample codes and any other related files are released at the following GitHub repository.
github.com
Input sample data: Weight of insect

Target sample data: Sex of insect

Sample data generation
The number of sample data is 50. The max value of
is 2.5 and the min value is 0. The target label
is male(1) or female(0). The each value of
and
is printed as follow.

A scatter plot of sample data is the following figure. The plot colored as gray is male and the other one colored as blue is female.

Policy to solve problem
The policy to solve this classification problem is to decide a boundary between male and female. This is called "decision boundary".
Classification with probability
In the above plot of sample data, if the weight was between 0.8g and 1.2g, the sex can be predicted with a probability including an ambiguity. For example, "The probability which the sex is male is 1/3". This probability depends on the weight, . In this case, the probability which the sex is male is called "Conditional probability" as follow.

Maximum likelihood estimation
For example, the target label at the first 3times are
and the label
at 4th time is
. According to this information, the following simple model is defined.

In this problem, "a probability which the target label data is generated from the above model". This probability is called "Likelihood". By Maximum likelihood estimation, the probability
which the likelihood is the most highest is calculated. The likelihood is expressed as follow.

The following plot is the calculated likelihood. The max likelihood is about 0.1055. And then, the probability which the sex is male is 0.25.

The male probability when the likelihood is maximum can be calculated as follow.

By taking the logarithm of the above likelihood model, the calculation can be easier. This is called "Log likelihood" and a purpose function for a probabilistic classification instead of mean square error. In this case, the parameter which maximizes the log likelihood need to be searched.
Logistic Regression
In almost cases, the data doesn't have a uniform distribution. The conditional probability can be expressed as "Logistic regression model" by assuming that it is generated from gaussian distribution.
The following model is logistic regression model. This is made by integrating linear line model with sigmoid function. An output is limited from 0 to 1 by passing the line model through the sigmoid model.

This plot is an example of the logistic regression model.

Cross entropy error
The probability which the label is 1 at a weight
is expressed as follow by using the logistic regression model.

This policy is what calculating the highest probabilistic parameter by assuming that the data is generated from the above model. In the case of , the probability is
. On the other hand, the probability of
is
. By considering both cases, the above model is expressed as follow. This is used for one data.

This is for data as "Likelihood".

This is "Cross entropy error" which the above function times same as mean square error. And then, "Mean cross entropy error" for data
is defined as follow. By this definition, it is difficult for the error value to be affected by the number of data.

The following 2 figures are all of calculated mean cross entropy error in changing the parameters of linear line model, and
. The left side figure is 3D contour map of mean cross entropy error and the right side figure is 2D contour map of one. According to these figures, the error is minimized at around point,
,
.

Calculating parameter by Gradient method
The parameters, and
can be calculated by Gradient method as follow.
The mean cross entropy error.

A partial derivative of at
.

is defined as follow. And then,
is called "Total input".

The partial derivative can be calculated with "Chain rule" as follow.

As result, the partial derivative of at
can be calculated as follow.
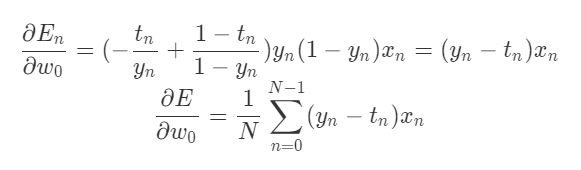
In the same way, the partial derivative of at
can be calculated as follow too.

As result, those parameters were calculated as follow.


According to the above contour map, the predicted parameters were ,
. The real calculated parameters were
,
. These parameters are close to the predicted ones.
Summary of classification sequence
1. Creating "Logistic regression model"
The model to output the probability which the target label as follow.

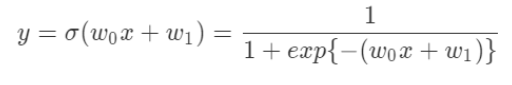

2. Defining "Likelihood"
By considering the above regression model, the likelihood per unit data is expressed as follow.

And then, "Log likelihood" for all of data is defined as follow.
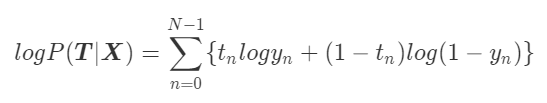
3. Defining "Mean cross entropy error"
The parameters of regression model can be calculated by minimizing the following error .

4. Calculating "Partial derivative" of 
The partial derivative at and
can be calculated as follow.

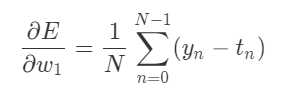
5. Calculating parameters by Gradient method
