Fundamentals of Classification by Supervised Learning ~2 dimensional input~

Table of Contents
Introduction
Author
GitHub
Generating sample data
2 classes classification
3 classes classification
Question

Introduction

I released the following article about 1 dimensional classification by supervised learning.
www.eureka-moments-blog.com
In this article, I wrote a memo about 2 dimensional classification into 2 or 3 classes. And then, I referred to the following book.

Pythonで動かして学ぶ！あたらしい機械学習の教科書第2版 (AI & TECHNOLOGY)

作者: 伊藤真
出版社/メーカー: 翔泳社
発売日: 2019/07/18
メディア: 単行本（ソフトカバー）
この商品を含むブログを見る

Author

researchmap.jp

GitHub

Sample codes and any other related files are released at the following GitHub repository.
github.com

Generating sample data

This data is 2 dimensional sample data. The following ones are first 5 data.
f:id:sy4310:20190814213619p:plain
This is 2 classes label data. The following ones are first 5 data.
f:id:sy4310:20190814213651p:plain
This is 3 classes label data. The following ones are first 5 data.
f:id:sy4310:20190814213725p:plain
This label data is created by setting 1 to only element at $k$ index in the target vector $t_n$ . This method is called "1-of-K coding scheme".
The following left side figure is 2 classification sample data plot. The following right side one is 3 classification sample data plot.
f:id:sy4310:20190814213424p:plain

2 classes classification

Logistic regression model on 2 dimension

This is a 2 dimensional logistic regression model. An output of this model $y$ is which approximates a probability $P(t=0|x)$ .
f:id:sy4310:20190821215344p:plain
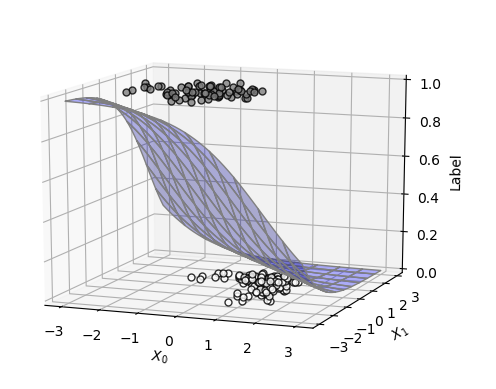
The following 2 figures are the output of this model in the case of $W=[-1, -1, -1$ ].
f:id:sy4310:20190821224819p:plain
f:id:sy4310:20190821224858p:plain

Mean cross entropy error

This following function can be used for mean cross entropy error same as the case of 1 dimension.
f:id:sy4310:20190822205538p:plain
And then, the partial derivative of this function can be calculated as follow.
f:id:sy4310:20190822210535p:plain

Calculating parameter by Gradient method

The following 2 figures of fitting result with 2 dimensional logistic regression model.
f:id:sy4310:20190822225926p:plain
The parameters $W$ was calculated by "Conjugate gradient method". According to the above right side figure, an accurate decision boundary was created with those parameters.
f:id:sy4310:20190822233315p:plain

3 classes classification

Logistic regression model for 3 classes classification

This regression model is defined with Softmax function.
www.eureka-moments-blog.com
Total input $a_k (k=0,1,2)$ is defined as follow.
f:id:sy4310:20190823215540p:plain
And then, by assuming the 3rd input $x_2 = 1$ , this formula is deformed as follow.
f:id:sy4310:20190823223401p:plain
This total input is used as input of the softmax function. An exponential function $exp(a_k)$ and the total of exponential function at each class $u$ are defined.
f:id:sy4310:20190823224705p:plain
$K$ is the number of class. In this case, $K=3$ . An output of softmax function is expressed with the above $u$ as follow.
f:id:sy4310:20190823225220p:plain
An output of this model is $y=[y_0,y_1,y_2$ ]. And then, $y_0+y_1+y_2=1$ . The parameter of model is expressed as the following matrix.
f:id:sy4310:20190823231306p:plain
Each output $y_0$ , $y_1$ , $y_2$ is expressed as a probability which the input $x$ belongs to each class as follow.
f:id:sy4310:20190823233638p:plain

Mean cross entropy error

"Likelihood" is a probability which all of class data $T$ is generated for all of input data $X$ . This is expressed as follow.
f:id:sy4310:20190824203532p:plain
The probability which all of label data was generated is calculated by the following formula.
f:id:sy4310:20190824203728p:plain
According the above formula, an mean cross entropy error is defined as follow.
f:id:sy4310:20190824204245p:plain

Calculating parameter by Gradient method

To calculate $W$ which minimizes $E(W)$ by Gradient method, a partial derivative of each $w_{ki}$ is used.
f:id:sy4310:20190824210602p:plain
The calculated parameters $W$ is this.
f:id:sy4310:20190824221517p:plain
The following figure is a fitting result by the logistic regression model with the above parameters.
f:id:sy4310:20190824221336p:plain
And then, the cross entropy error is 0.26.