はじめに
前回は、指数関数と対数関数の応用編としてシグモイド関数・ソフトマックス関数編を記事にしました。
今回は、このシリーズの最後として、ガウス関数について勉強した事のメモになります。
参考書籍
本記事の内容は、下記の書籍を読んで要点を抽出し、メモしたものになります。

- 作者: 伊藤真
- 出版社/メーカー: 翔泳社
- 発売日: 2018/01/24
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (3件) を見る
ガウス関数とは
ガウス関数は下記の数式で表され、曲線を近似する基底関数として用いられる。
グラフで描くと、下記のような形となる。
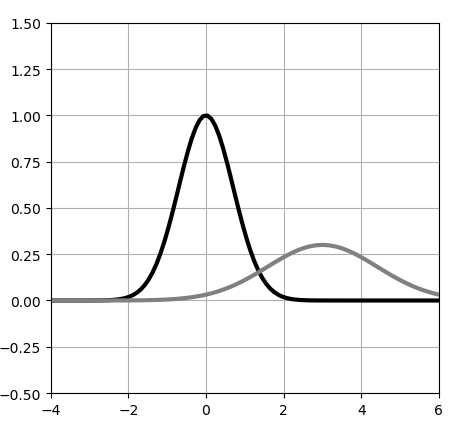
中心(平均)を、左右の広がりの大きさ(標準偏差)を
、高さをaで表している。確率分布を表すのにガウス関数が用いられる場合は、aの部分を下記のようにする。
2次元への拡張
入力を2次元ベクトルとした場合、ガウス関数の形は下記のような式になる。
また、グラフで描くと下記のようになる。

関数の形を表すパラメータを加えた2次元ガウス関数
高さのa、平均(中心)ベクトルの、共分散行列の
をパラメータとして加えた場合、2次元ガウス関数は下記のような形となる。
またこの時、共分散行列のは、下記のような2×2の行列になる。
この行列要素のと
は、
方向と
方向の分布の広がりを表す。
は、分布の傾きである
と
の相関に対応しており、正なら右上がり、負なら左上がりの分布を表現する。
高さaは、関数の大きさを決めるパラメータと考えられるが、ガウス関数で確率分布を表す場合はには、下記の形でセットされる。
こうすることで、入力空間での積分値が1となり、関数が確率分布を表現できるようになる。式中になるは、
の行列式であるので、今回のような2×2の行列の場合には、下記のように計算できる。
ここで、パラメータである平均(中心)ベクトル、共分散行列
を、
とした場合、これによる2次元ガウス関数のグラフは下記のようになる。

サンプルコード
ここまで記載した各グラフを作成するPythonのサンプルコードは下記のGitHubリポジトリで公開しています。