目次
- 目次
- はじめに
- 予測モデルの学習手法の選定:Linear SVC
- とりあえずやってみる
- データを正規化・標準化してみる
- Z-Score Normalization(標準化)
- Min-Max Normalization
- データの分布形状を確認
- 正規化・標準化したデータで再度Linear SVC
- 次のステップ
はじめに
以前、カリフォルニア大学アーバイン校(UCI)が公開している「ワインの等級を予測するための学習データサンプル」を用いたデータ分析についての記事を書きました。
今回はその続きとして、データの分析結果に基づいて実際に等級予測を行ってみたので、その結果を紹介しようと思います。
また今回は、単にデータを学習させるだけではなくて、機械学習において重要とされるデータの正規化・標準化も考慮しながら行ってみました。
予測モデルの学習手法の選定:Linear SVC
学習手法は数多くありますが、今回はPythonの機械学習ライブラリであるscikit-learnのアルゴリズムチートシートに基づいて手法を選定してみました。

Startから始まり以下の流れに沿って進んだ結果、Linear SVCで学習させるという事になりました。
Start
↓
サンプル数は50以上か: YES
↓
予測するのはカテゴリか: YES
↓
サンプルデータはラベル付けされているか: YES
↓
サンプル数は10万以下か: YES
↓
Linear SVC
Linear SVCによる学習については、以下の記事で詳しく説明されています。
sklearn.svm.LinearSVC — scikit-learn 0.24.2 documentation
http://www.sist.ac.jp/~kanakubo/research/neuro/supportvectormachine.htmlwww.sist.ac.jp
とりあえずやってみる
前回のデータ分析より、以下の散布図のようにColor intensity(色彩強度)とProline(プロリン)という2次元の特徴量を用いれば、ワインの等級1~3を判別することが出来そうだということがわかりました。
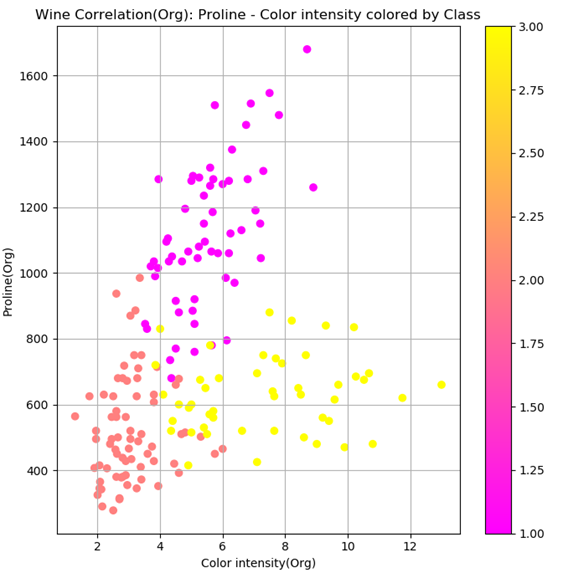

まずはこのまま、何の正規化や標準化もしない状態でLinear SVCによる学習と、それによる等級予測を行ってみました。学習の際には、全サンプルデータ178個をランダムで学習用データと検証用データに振り分け、全体の4割が検証用データとなるようにしました。
その結果が以下になります。
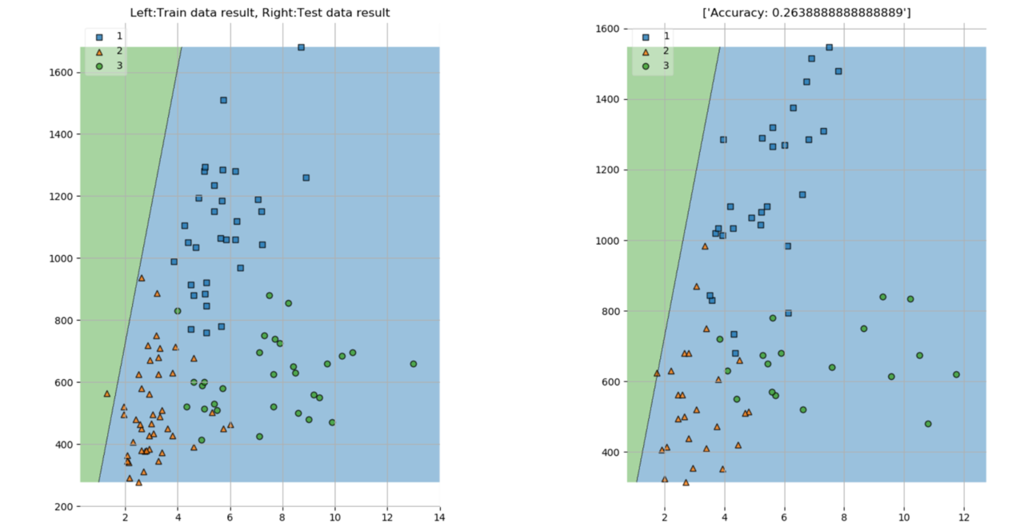
左が学習用データの散布図、右が検証用データの散布図であり、それぞれにLinear SVCで学習された識別線を引いたものです。見て分かる通り、識別したい等級が3つであるにもかかわらず識別線が一本しか引かれていません。また、その識別線が引かれている場所も明らかにおかしいですね。検証用データに対する識別精度も26%と散々な結果でした。
データを正規化・標準化してみる
以下の記事にて説明されているように、データに対する計算やデータ同士の比較をしやすくするために正規化・標準化は非常に重要です。今回の学習で特徴量とした色彩強度とプロリンでは取り得る値の範囲が違いすぎるので、正規化・標準化によってスケールを合わせてやらないと、上記の結果のように識別精度が低いモデルが学習されてしまうのかもしれません。
webbeginner.hatenablog.com
st-hakky.hatenablog.com
データを正規化・標準化するにあたり、今回は一般的な以下の2つの手法を用いて、それによる予測精度の比較をしてみました。
Z-Score Normalization(標準化)
元データを平均0、標準偏差1に変換する手法であり、外れ値のあるデータに対して有効。最大値、最小値に上限、下限がない場合に使うと良い。データの分布形状がガウス分布になっていることが前提。
この手法で標準化したデータの散布図は以下のようになる。

Min-Max Normalization
最小値を0、最大値を1とする正規化手法であり、最大値と最小値が予め決まっている様な場合に有効。外れ値が存在していないことが必要。外れ値があるとそれに引っ張られて正規化が上手くいかない。データが一様分布であることが前提。
これにより正規化したデータの散布図は以下のようになる。

データの分布形状を確認
上記の2つの正規化・標準化では、それぞれデータの分布形状にガウス分布 or 一様分布という条件があります。なので、順番が逆な気がしますが、特徴量とする色彩強度とプロリンの数値がどのように分布するのかを確認してみました。
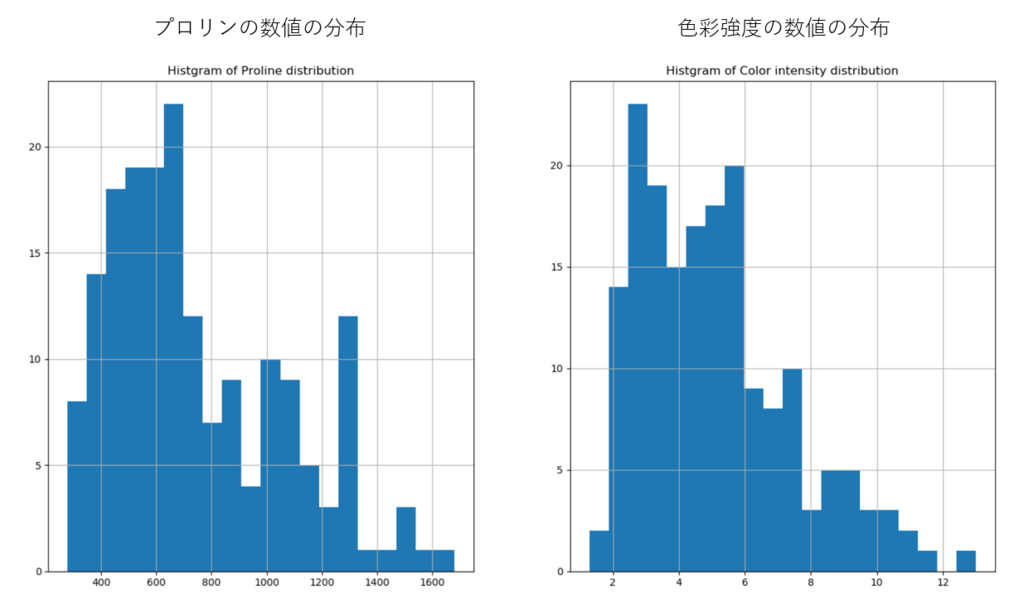
左がプロリン、右が色彩強度ですが、どちらかと言えば両者とも正規分布に近い形状をしているようです。なので、Z-Score Normalizationで標準化した場合の方が識別精度は高くなるのかもしれません。
正規化・標準化したデータで再度Linear SVC
まずはZ-Score Normalizationで標準化したデータによる学習と、それによる予測精度は以下のような結果になります。

元のデータで学習した時と比べて、まずは3つの等級を識別した線がちゃんと引かれるようになりました。予測精度も86%となかなか高い結果です。右側散布図の検証用データに対する識別結果を見ると、各等級のデータが重なり合っている(0, 0)付近で一部のデータが別の識別領域に入り込んでいることがわかります。この辺はやはり線形の識別では完全に分離するのは難しいようです。
続いて、Min-Max Normalizationで正規化した場合の結果は以下。

これもちゃんと3つの等級を識別する線がちゃんと引かれました。ただし予測精度は84.7%と悪くはないですが、Z-Score Normalizationの86%を若干下回る結果となりました。
両者の違いを見ると、等級2と3の間に引かれる識別線の位置に大きな違いが見られます。Min-Max Normalizationでは、左側散布図における学習用データに対する識別線が、等級3のデータの一部を等級2と識別してしまうように引かれていますが、この誤識別されるデータ数が明らかにZ-Score Normalizationの場合よりも多くなっているように見えます。ここが精度の違いに影響しているようです。
次のステップ
元のデータを正規化・標準化することで、Linear SVCによる等級予測ができるようになることが分かりました。また、Z-Score NormalizationとMin-Max Normalizationとの間で予測精度に差が生まれることも分かりました。
識別できるようになることは分かりましたが、これらの結果がどのようにして導き出されたのかは正直まったくわかっていません。パラメータのチューニングは特に行っていないし、以下の記事にもあるようにSVMを使いこなすにはまだまだ理解するべき事が沢山ありそうです。
今後は、パラメータチューニングによって結果がどう変わるのかを検証したり、SVMの中身を詳細に理解することに取り組んでみようと思います。
