目次
はじめに
以前、機械学習に必要な数学について学んでいくにあたり、下記の記事を書きました。
今回はその続きとして、行列についての基本を勉強したので、そのメモを記事にします。
行列とは
数字を縦か横に並べたものを「ベクトル」と呼ぶが、縦にも横にも表のように並べたものを「行列」と呼ぶ。行列を使うと、沢山の連立方程式を一つの式で表すことができ、とても便利である。
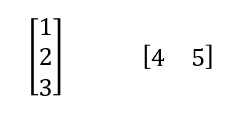
また、ベクトルも行列の一種とみなすことができる。例えば、下記左の式の縦ベクトルは3行1列の行列であり、下記右は1行2列の行列とみなせる。
Pythonにおける行列の定義
行列を定義するときには、まず行ごとに[ ]でくくり、更に全体を[ ]でくくるという二重の構造にする。例として、下記のように定義になる。
import numpy as np # In A = np.array([[1, 2, 3], [4, 5, 6]]) # Out [[1 2 3] [4 5 6]]
行列の積
下記式のような1 × 3の行列Aと3 × 1の行列Bを考える。
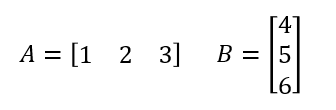
そして、この2つの行列の積は下記のようになる。
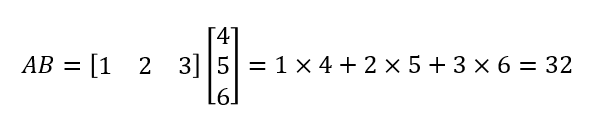
これは、AとBをベクトルとみなした場合の内積とも考えることができる。また、Pythonではベクトルの内積を下記のように計算できる。
# In A = np.array([1, 2, 3]) B = np.array([4, 5, 6]) A.dot(B) # Out 32
このようなA.dot(B)は内積に限ったものではなく、行列積を計算する演算である。Pythonの行列積は、計算が可能なように行列の向きを自動で調整してくれる。よって上記のようなコードでは、Bが横のベクトルとして定義されていても、Pythonが自動で縦ベクトルと解釈して計算する。
単位行列
対角成分が1でそれ以外が0である特別な正方行列をIで表し、それは単位行列と呼ばれる。Pythonでは、下記のコードでn×nの単位行列が生成される。
# In 3×3の単位行列 np.identity(3) # Out [[1. 0. 0.] [0. 1. 0.] [0. 0. 1.]]
単位行列は、スカラーでいうところの"1"に似ている。サイズが同じ正方行列であれば、どのような行列を掛けても行列は変化しない。
逆行列
サイズが等しい正方行列に限り、掛けると単位行列になる行列を逆行列という。
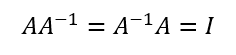
例えば、2×2の行列の場合は下記の公式で逆行列が計算できる。
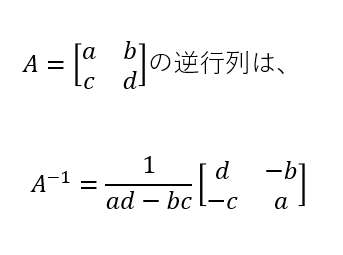
また、Pythonでは下記のようなコードで逆行列を求める事ができる。
# In A = np.array([[1, 2], [3, 4]]) inv_A = np.linalg.inv(A) # Out [[-2. 1. ] [1.5 -0.5]]
ちなみに、上記の公式においてad-bc=0となる場合は0割りが起きてしまうので、逆行列は存在しないということになる。
3×3行列の逆行列を求める
上記の公式では3×3から上のサイズの逆行列を求めることは計算が面倒なので、別の求め方として、余因子を用いた計算方法がある。

ここで、detAはAの行列式、ΔijはAのi行目とj列目を除いた行列の行列式に(-1)のi+j乗を掛けたものであり、余因子と呼ばれる。計算例を下記に示す。

転置
上記の逆行列と合わせて、転置行列の計算はロボティクスや機械学習の理論式を理解するのに必須である。転置行列とは行と列を入れ替えた行列であり、例えば

となる。また、転置にすると行列積の順番が逆になるという性質がある。Pythonでは下記のコードで計算できる。
# In A = np.array([[1, 2, 3], [4, 5, 6]]) A.T # 転置 # Out # オリジナル [[1 2 3] [4 5 6]] # 転置 [[1 4] [2 5] [3 6]]
行列と写像
ベクトルの足し算や引き算に図形的な解釈があるように、行列にも図形的な解釈がある。行列は「ベクトルを別なベクトルに変換する規則」として解釈できる。ベクトルという数字の組を”座標”と解釈すれば、それは"空間内のある点"とも解釈できるので、行列は「ある点を別な点に移動させる規則」として捉えることもできる。
グループ(ベクトルや点)からグループ(ベクトルや点)への対応関係を与える規則を写像といい、行列は線形写像というタイプに分類される。例として、下記のような行列の写像を考える。
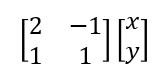

また、先述した逆行列を用いて、ある行列による写像で移動した点から移動前の点を求めることもできる。その例を下記に示す。

次回の内容
次回は指数、対数編を書こうと思います。
