
- 作者:友納 正裕
- 発売日: 2018/03/03
- メディア: 単行本(ソフトカバー)
目次
目的
- 書籍「SLAM入門」を参考に、SLAMを実行する際に効果的なスキャンデータの前処理について理解する。
- サンプルコードを参考に、C++での設計思想について理解する。
前処理の手法
- 基本的には現在時刻に観測されたスキャンデータをそのまま用いるが、下記のような前処理を施す事によりSLAMの精度や処理時間が改善される場合がある。
スキャン点間隔の均一化
- スキャンレーザは等角度間隔で放射線状にレーザを照射するため、遠くの物体である程スキャン点群の密度が低くなる。
- スキャンマッチングは、スキャン点の平均でコストを計算するため、低密度な部分の影響は小さくなる。
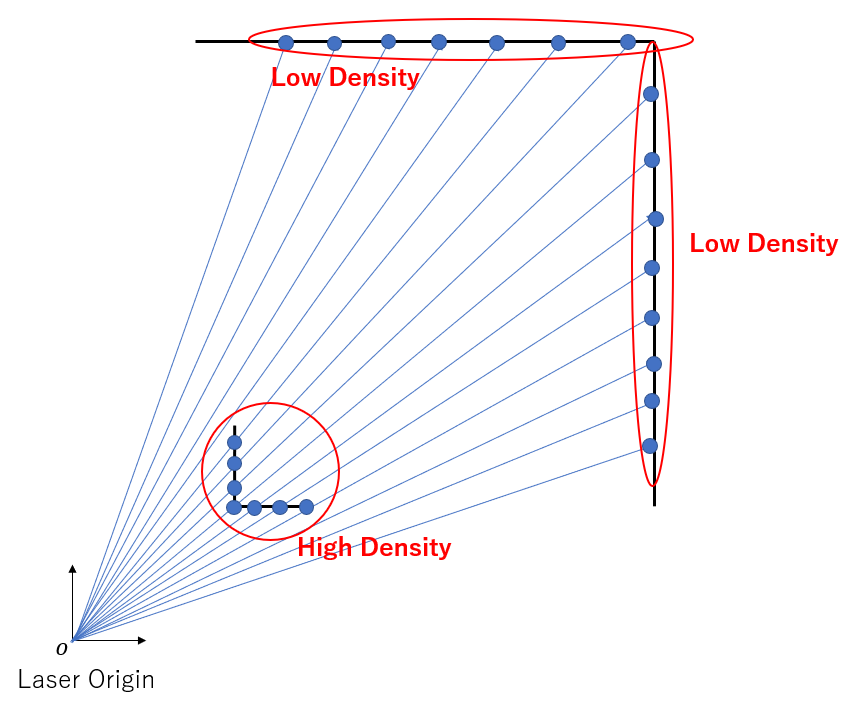
- 低密度なスキャン点群も使って広い形状マッチングする方が精度は上がる。
- 各スキャン点の間隔を均一にする事で、点群密度を均一に出来る。
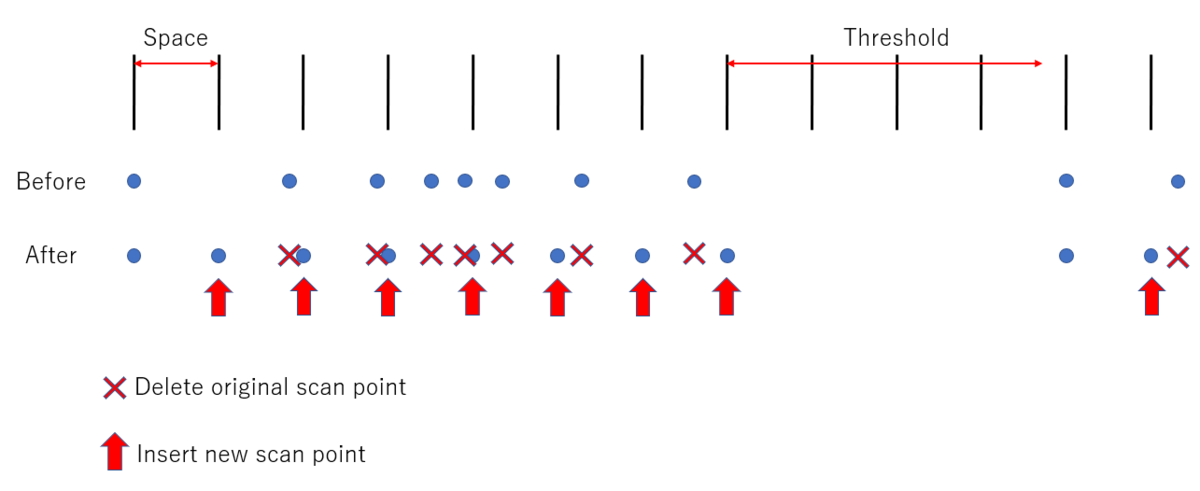
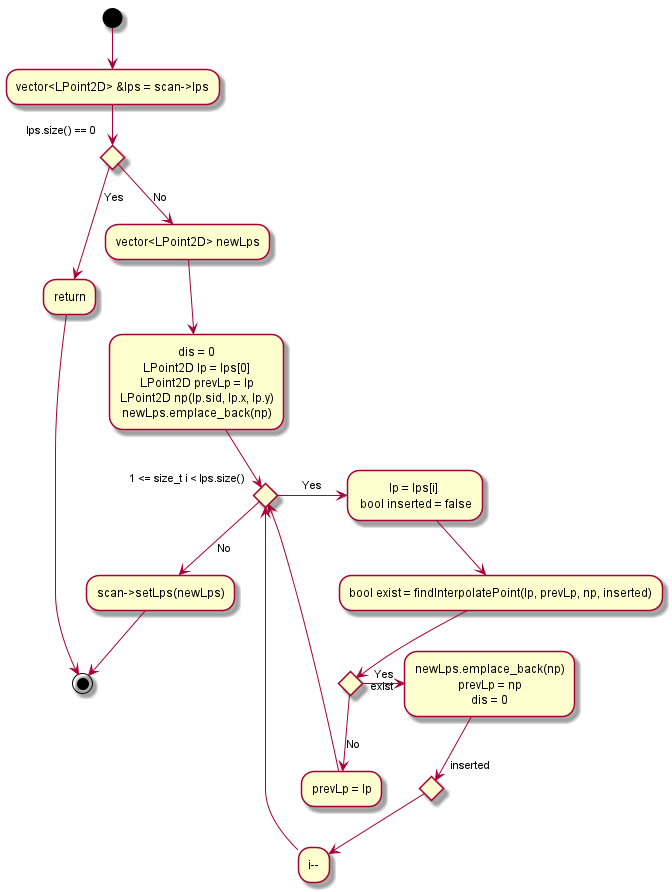
- 等間隔でスキャン点が並ぶように新しいスキャン点を挿入し、元の点は削除する。
- 一つ前の点との距離が閾値を超えた場合は、そこまでの間にはスキャン点が一切無いとして、今注目している点をそのまま採用する。
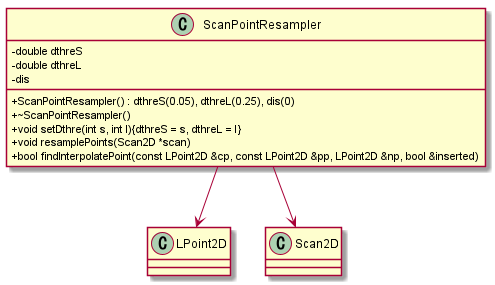
クラス設計
- 各スキャン点の間隔は0.05m、スキャン点が無いと判断する閾値は0.25mに設定。
- Resamplerという名前は果たして適切なのか。もう少し「スキャン点を均一に並べる」という責務が分かりやすい名前が良さそう。
メソッド設計
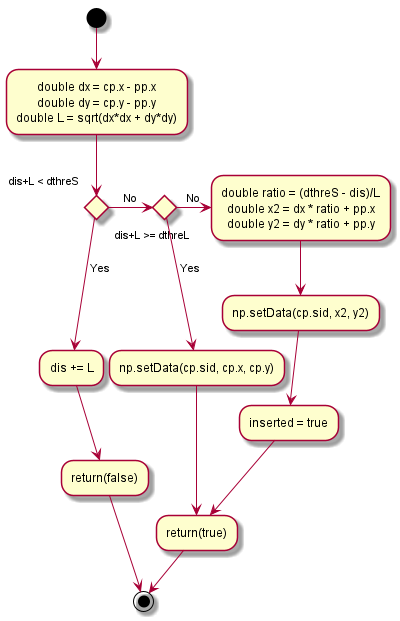
- findInterpolatePoint()
- スキャン点間の距離を閾値処理し、もとの点を残すか削除するかを判定する。
- 新たに点を挿入するならば、その点の座標値を計算する。
- resamplePoints()
- 各スキャン点の維持、削除、挿入処理を行い、最終的に間隔が均一に調整されたスキャン点群データを生成する。
スキャン点の法線の計算
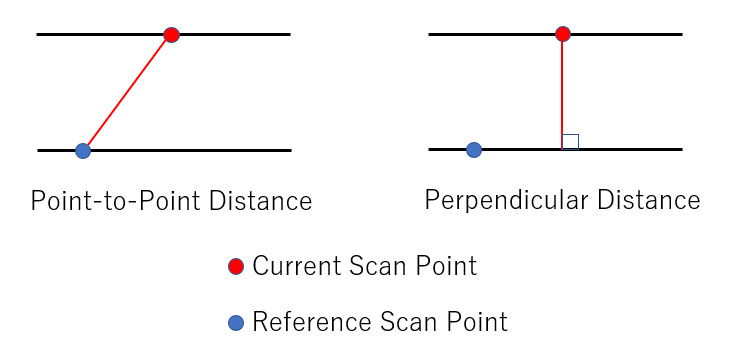
- ICPアルゴリズムによるスキャンマッチングでロボット位置を最適化する際は、一般的には下図左のように現在スキャン点(赤)と参照スキャン点(青)の2点間距離を用いてコスト関数を定義するのが一般的。
- ただし、平面が多い環境では下図右のように現在スキャン点から参照スキャン点の接線に下した垂線の長さ(垂直距離)をコスト関数に利用する方が、マッチング精度が良くなる傾向がある。
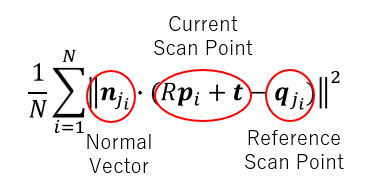
- 垂直線を用いたコスト関数の定義。
- このコスト関数を計算するために、参照スキャン点の法線ベクトルが必要になる。
- 垂直距離で用いる垂線は、この法線ベクトルと平行とする。
クラス設計
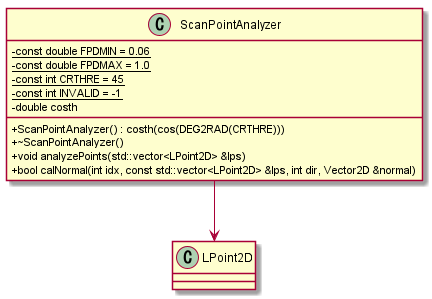
- 注目する一点とその近傍にある点とで構成する法線ベクトルを計算する。
- 2点間の距離が近すぎたり、遠すぎたりしないようにFPDMINとFPDMAXで制限をかける。
- これもクラス名からでは責務がよく分からない。NormalVectorCalculatorくらいがいい気がする。
メソッド設計
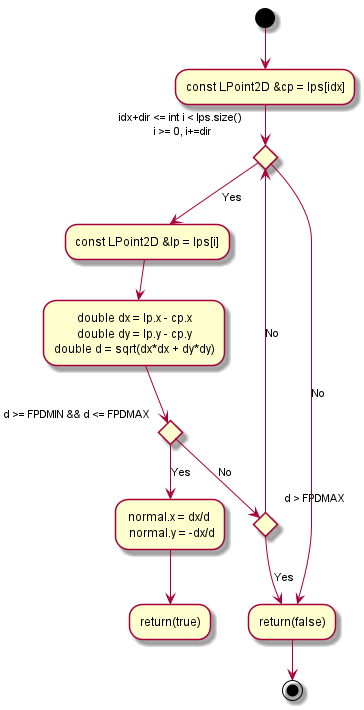
- calNormal()
- 指定した2点で法線ベクトルを計算する。
- お互いの距離が近すぎる or 遠すぎる場合は法線ベクトルの誤差が大きくなるので計算しない。
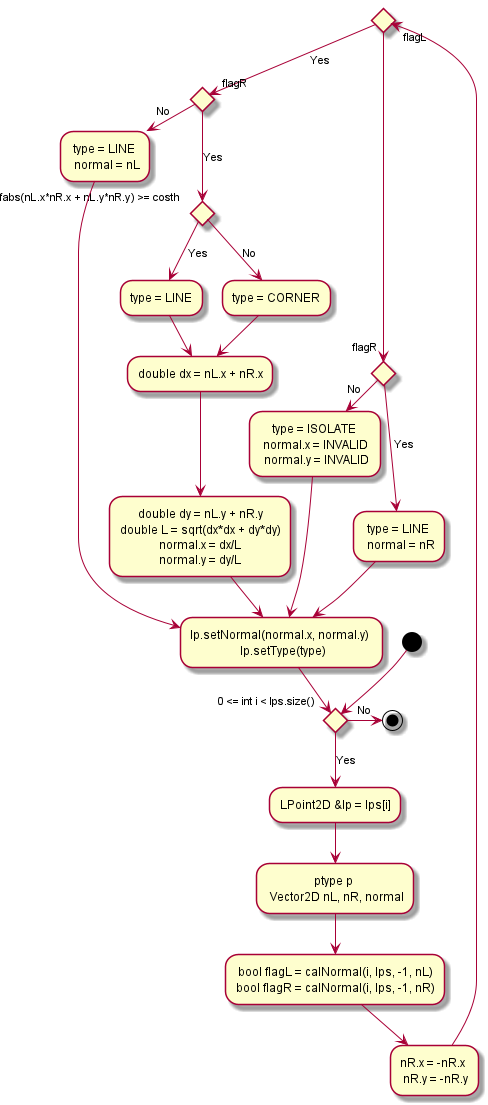
- analyzePoints()
- 左右の近傍点でそれぞれ法線ベクトルを計算する。
- それらの方向の食い違いにより、今の注目点がコーナー点かどうか判定する。
GitHub
記載されているUMLのダイアグラムは、全て下記のGitHubで公開済み。