構造化データを前処理する際のPython逆引きメモ

機械学習のための「前処理」入門

目的

データ分析の仕事をする際は、Pythonで専用のスクリプトを書いたりして
実施することがほとんどですが、自分がやりたい処理をするのに未だに
pandasやnumpy, matplotlibなどの使い方を調べたりすることがあります。
今回は、csvファイルを読み込んだときのような構造化データを処理する
際によく使うコードを、今後すぐ思い出せるようにメモに残しておこうと
思います。

目次

DataFrameの各項目型やメモリサイズを確認する

例えばこういう内容のDataFrameがあった場合、

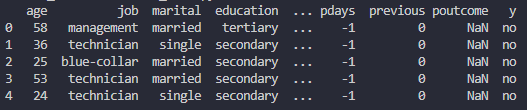
このようなコードで確認できます。

df.info()

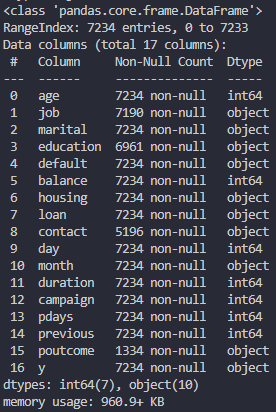
DataFrameに欠損値が含まれているか調べる

行方向の欠損値の有無

df.isnull().any(axis=1)

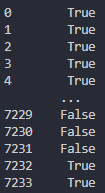
列方向の欠損値の有無

df.isnull().any(axis=0)

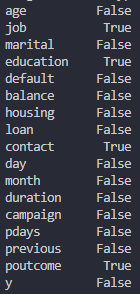
DataFrameに含まれる各データの統計量を計算する

df.describe()

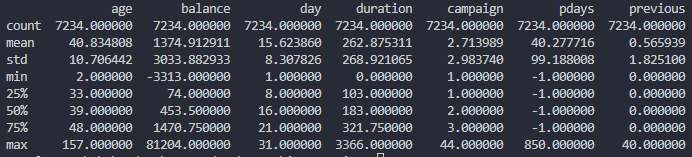
ここで計算される統計量の中にある25%, 50%, 75%というのは、
四分位数における第一四分位、第二四分位、第三四分位のこと
を指します。

データ間の相関係数を計算する

データフレームに含まれるageとbalanceという二つのデータの
相関係数を計算する場合、こちらのコードで計算できます。

df[["age", "balance"]]

各データの出現数をカウントする

一覧でぱっと確認したい場合はこちら。

df["job"].value_counts(ascending=False, normalize=True)

ascendingは、計算された出現率を昇順にソートするかどうかであり、
Falseにすると降順になります。normalizeは、出現数の合計が1となる
ように正規化するかどうかであり、Trueにすると比率になります。

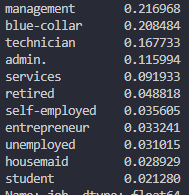
また、こうするとラベル情報だけを取り出せます。

df["job"].value_counts(ascending=False, normalize=True).index

こうすると計算された出現率だけを取り出せます。

df["job"].value_counts(ascending=False, normalize=True).values

欠損値を除外する

欠損値が多い/少ないを判断する一つの目安として、
それが全体の3分の1以上あれば多いと考えるのが
一般的なようです。
例えば、ある特定のデータ列に注目して、その中にNanと
なっている行があれば、それを次のコードでデータフレーム
から削除できます。

df = df.dropna(subset=["job", "education"])

欠損値を補完する

欠損値を意味するNanが含まれている場合、それを0や
その他の定数、前後の値、平均値で補完したくなります。
また、これが文字列の場合なら、ある別の文字列で
補完する方がいいです。

例えば、このようにNanを含んだ文字列のデータ列が
ある場合、

こちらのコードによって指定の文字列(ここ
では"unknown")に置き換えることができます。

df = df.fillna({"contact": "unknown"})

こうすることで、Nanが"unknown"に補完されます。

文字列を数値へ置き換える

ここで処理したデータを機械学習のアルゴリズムに入力する
には、文字列のデータを数値に変換しておく必要があります。
例えば、"ys"と"no"といった2パターンの文字列であれば、
"yes"を1、"no"を0としてこちらのようなコードで置き換える
ことができます。

df = df.replace("yes", 1)
df = df.replace("no", 0)

ただし、必ずしも上記のような2値データばかりではなく、
より多くのパターンがある多値データの場合もあります。
そういうときは、こちらで解説されてるようなOne-hot表現
により数値に変換することができます。
mathwords.net そして、pandasに備わっているget_dummies()により
簡単にOne-hot表現による変換ができます。

df_job = pd.get_dummies(df["job"])

この場合だと、"job"という項目のデータ列に含まれる
こういった複数パターンの文字列を、

このような0と1の数値の組み合わせに変換してくれます。

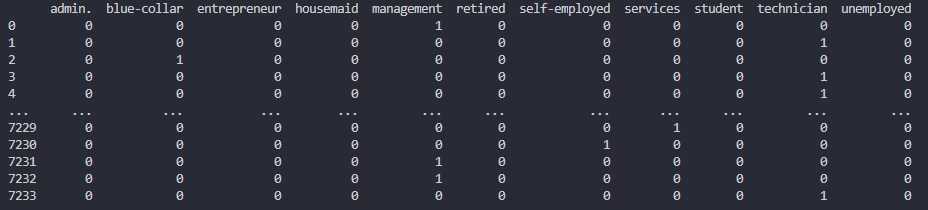
不均衡データを均衡化する

不均衡データとは、データ構造に偏りがあり、正例または負例
データの片方が極端に少ないデータ群のことです。
例えばこのようにある二つのクラスに分類されるデータがあると
します。

X = np.array(bank_df_new.drop('y', axis=1))
Y = np.array(bank_df_new[['y']])
print(np.sum(Y == 1), np.sum(Y == 0))

ここでの出力は、1となるデータの数が820に対して、0となる
データの数が6113と極端に多いです。このままだと、0となる
ものだけを検出できる極端な機械学習モデルが作られてしまう
のでよくありません。

qiita.com

こういう場合は、それぞれのデータ件数を均衡にすることで
偏りのないデータ群にしてやる必要があります。このための
手法として簡単なのは、「多数クラス(0)のデータ件数を、
小数クラス(1)のデータ件数と同じにする」ことです。
具体的には、「多数クラスのデータをシャッフルし、小数
クラスと同じ件数分のデータを抽出する」というやり方
です。これを、「アンダーサンプリング」といいます。

Pythonでは、imbalanced-learnというライブラリを使えば、
こちらのコードで簡単にアンダーサンプリングを実行する
ことができます。

import numpy as np
from imblearn.under_sampling import RandomUnderSampler

sampler = RandomUnderSampler(random_state=42)
X, Y = sampler.fit_resample(X, Y)
print(np.sum(Y == 1), np.sum(Y == 0))

これにより、先程の不均衡データをそれぞれのクラスの
データ件数が小数クラスと同じ820件ずつに揃えることが
できます。

ただし、このように極端に多数クラスのデータ件数を
削減してしまうと、モデル作成に必要なデータ件数が
不足してしまい、高い予測精度が得られにくくなります。
そういう場合は、逆に「オーバーサンプリング」という
手法を使い、小数クラスのデータ数を水増しさせる
こともできます。

import numpy as np
from imblearn.over_sampling import RandomOverSampler

sampler = RandomOverSampler(random_state=42)
X, Y = sampler.fit_resample(X, Y)
print(np.sum(Y == 1), np.sum(Y == 0))

文字列を集約する

いろんなパターンの文字列になり得るデータがあるとき、
それらをある条件に基づいてより少ないパターンに
まとめたくなるときがあります。
例えばこちらのコードだと、いろんなパターンの職業を
文字列で記録したデータに対して、"worker"と"non-worker"の
2パターンに集約できます。また、それをまた新たなデータ列
である"job2"としてデータフレームに追加しています。

df.loc[(df["job"] == "management") |
        (df["job"] == "technician") |
        (df["job"] == "blue-collar") |
        (df["job"] == "admin") |
        (df["job"] == "services") |
        (df["job"] == "self-employed") |
        (df["job"] == "entrepreneur") |
        (df["job"] == "housemaid"), "job2"] = "worker"

df.loc[(df["job"] == "retired") |
        (df["job"] == "unemployed") |
        (df["job"] == "student"), "job2"] = "non-worker"

データを正規化する

正規化とは、データのスケール(単位)を扱いやすいものに変換し、
スケールの異なる変数同士を比較できるようにすることです。

正規化の手法としてまずよく使われるのが範囲変換です。
これは、正規化された後の変数の最小値が0、最大値が1となる
ようにする手法です。それを実行するPythonコードはこちらの
ようになります。

from sklearn.preprocessing import MinMaxScaler

mc = MinMaxScaler()
mc.fit(df)
df_mc = pd.DataFrame(mc.transform(df), columns=df.columns)
print(df_mc)

また、範囲変換と同様によく使われる手法としてZ変換があります。
これは、正規化された後の変数の平均値が0、標準偏差が1となる
ようにする手法です。それを実行するPythonコードはこちらの
ようになります。

from sklearn.preprocessing import StandardScaler

sc = StandardScaler()
sc.fit(df)
df_sc = pd.DataFrame(sc.transform(df), columns=df.columns)
print(df_sc)

atmarkit.itmedia.co.jp

データをグループ化する

関連の強いデータ同士をまとめて複数のグループに分けることを
クラスタリングといいます。その中でまず一般的なのは、距離が
近いデータから順に併合していく階層クラスタリングという手法
です。
www.albert2005.co.jp この記事でも紹介されているウォード法というデータの併合
方法を使った階層クラスタリングをこちらのPythonコードで
実行できます。

from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt

hcls = linkage(df, metric="euclidean", method="ward")
dendrogram(hcls)
plt.show()

実行すると、このように各データを階層型に結び付けた図が
表示されます。この図はデンドログラムと呼ばれます。

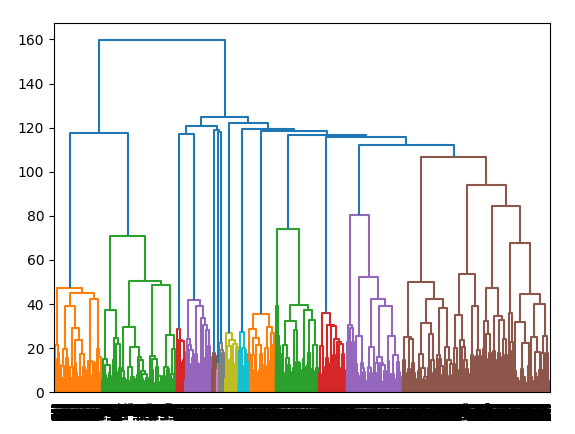
また、こちらのコードを実行すると、データをユークリッド
距離で閾値100でグループ化し、各データがどのグループに
分けられたのかを示すID番号の配列を得ることができます。

from scipy.cluster.hierarchy import fcluster

hcls = linkage(bank_df_sc, metric="euclidean", method="ward")
cst_group = fcluster(hcls, 100, criterion="distance")
print(cst_group)

これは、今後また新たな特徴量として利用できるものです。

また、もう一つの一般的な手法として非階層クラスタリング
があります。そして、この手法の一種としてk-Means法が
というものが有名です。

www.albert2005.co.jp

これは階層クラスタリングと異なり、あらかじめいくつの
グループに分けるかを決め、決めた数の塊にサンプルを
分割するというものです。Pythonではこちらのコードで
実行できます。

from sklearn.cluster import KMeans

kcls = KMeans(n_clusters=10)
cst_group_k = kcls.fit_predict(df)
for i in range(10):
    labels = df[cst_group_k == i]
    plt.scatter(labels["age"], labels["balance"], label=i)
plt.legend()
plt.xlabel("age")
plt.ylabel("balance")
plt.show()

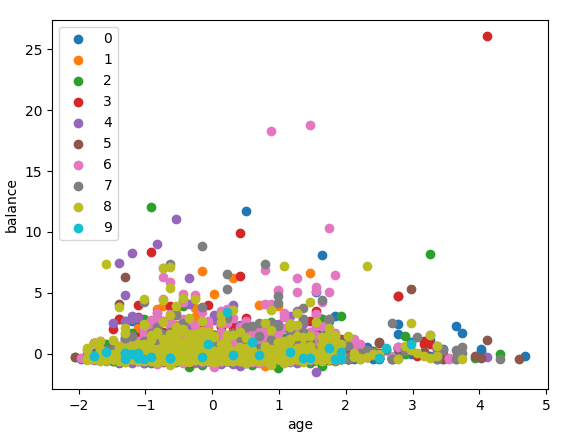
実行すると、このようにクラスタIDごとに色分けされた
散布図が出力されるはずです。

主成分分析

主成分分析とは、多種類のデータを要約するための手法です。
画像や時系列データのように変数の数が多いデータが
ある場合、その変数のデータ全てを見なくても全体の特徴を
掴むことができます。
また、そういった複数の変数を1つにまとめて新たな変数として
扱うことができるようにもなります。
logics-of-blue.com

例えば、こちらのPythonコードを実行すると、
累積寄与率が80%に達するまでの主成分を抽出する
ことで、データ列数を圧縮できることを確認できます。

from sklearn.decomposition import PCA

pca = PCA(0.80)
df_pca = pca.fit_transform(df)
print(pca.n_components_)
print(df_pca)

実行結果を見ると、もともとのデータ列数よりも
主成分分析後のデータ列数の方が少なくなっている
のがわかると思います。

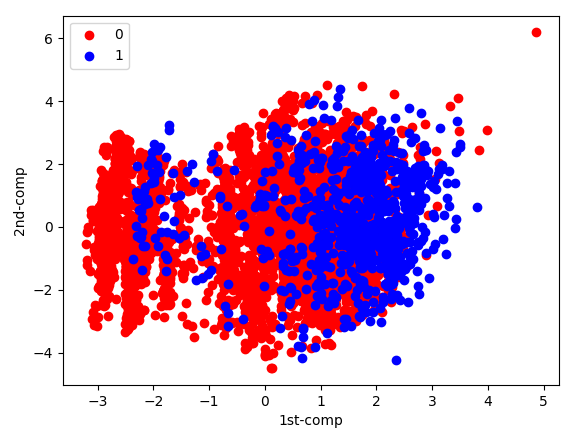
また、このようなコードにすると、
特定の目的変数における第1主成分と
第2主成分の分布を確認することができます。

import matplotlib.pyplot as plt

# extract 'y' as target variable
y = df['y']

# create new variable by principal component analysis
pca = PCA(0.80)
df_pca = pca.fit_transform(df)
df_pca = pd.DataFrame(df_pca)
df_pca['y'] = y

# draw scatter of 1st component and 2nd component about 'y'
df_pca_0 = df_pca[df_pca['y'] == 0]
df_pca_0 = df_pca_0.drop('y', axis=1)
plt.scatter(df_pca_0[0], df_pca_0[1], c="red", label=0)
df_pca_1 = df_pca[df_pca['y'] == 1]
df_pca_1 = df_pca_1.drop('y', axis=1)
plt.scatter(df_pca_1[0], df_pca_1[1], c="blue", label=1)
plt.legend()
plt.xlabel("1st-comp")
plt.ylabel("2nd-comp")
plt.show()

実行するとこのような散布図が出力されるはずです。