
- 作者:涌井 貞美
- 発売日: 2017/09/14
- メディア: Kindle版
目次
背景・目的
以前、こちらの記事で紹介したように、
卓球の試合の勝率の推移をシミュレート
するPythonプログラムを作りました。
なんとなくそれっぽくなっていますが、
計算された勝率が100%あるいは0%に
なる部分がちらほら見られ、実際の
試合とはまだまだギャップがある
状態です。
この計算精度を上げるべく、今回は
ベイズ推定による確率の推定を検討
してみたので紹介します。
スポーツにおけるベイズ推定
ベイズ推定とは、ベイズの定理に
基づいて、事前に立てた仮説が
どのくらいの確率で成立するかを
様々な条件を考慮しながら推定
する手法です。
スポーツの場合だと、例えばこの
記事にあるような試合の勝敗予想
に用いられます。
過去の対戦成績などから大体の
勝率を予測し、そこに天候や
会場の状態、戦術、選手の
コンディションなどを反映させ
ながら予測した勝率をどんどん
更新して精度を高めるという
ものです。
卓球の試合で予測したい確率とは
卓球の試合データを分析する際に、
予測したくなる確率の種類は下記の
ようなものが考えられます。
- 試合の勝率
- 得点率
- 失点率
前回の記事では勝率を予想して
いましたが、ここ最近では得点率
を予測する事こそが一番重要
なのではないかと考えています。
選手は試合の中で相手の出方を
予測した上でプレーし、実際の
プレーの結果から自分の予測を
逐次更新していくはずです。
そしてその中で、自分が得点できる
確率が一番高い戦術を選択していく
でしょう。
失点率も予測したくなりますが、
失点以上に自分が得点すれば良い
と前向きに考えれば、そこまで
重要ではありません。
また、得点率が高い選択をして
いけば自ずと勝率もついてくると
思うので、ここから先は自分の
得点率をベイズ推定で予測して
いく事を考えていきます。
得点率を予測する一連の流れ
得点率を予測する理論を立てるに
あたり、実在する卓球選手の統計
データを例として取り上げます。
元になるデータは、2019~2020年
にかけて行われたTリーグの現時点
までの全試合のスタッツです。
この中から2人の選手AとBを選び、
Aが自身の過去の戦績と、対戦相手
であるBの過去の戦績を考慮しながら
次にまた対戦する際の自身の得点率
を予測するものとします。
まず、自身の得点率を予測したい
選手Aとなるのは神巧也選手です。
次に、対戦相手Bとなるのは、
吉村真晴選手です。
0. 戦術の分類を定義する
自身の得点率を予測するための
手がかりになるのは、相手が
取るであろう戦術と、自身が
取るべき戦術です。
この戦術をいくつかのパターン
に分類しなければなりませんが、
今回はざっくりと下記の4パターン
の戦術をそれぞれに取り得ると
します。
- サーブ→3球目の間で得点
- 5球目 or 以上のラリーで得点
- レシーブ→4球目の間で得点
- 6球目 or 以上のラリーで得点
1. 相手が各戦術を取る事前確率を定義する
自分が取るべき戦術を決めるために、
まずは相手がどの戦術を取る確率が
高いかを考えます。
戦術1~4という条件を~
と
して、それぞれが取られるであろう
確率を~
とします。
これらは、得失点にかかわらず、相手が
全試合の中で各戦術を実行した割合に
相当します。
これらは事前確率と呼ばれ、ベイズ
推定ではこの事前確率をいろんな
情報を反映させながら更新し、
精度を向上させる事になります。
今回は相手の過去の成績が分かるという
前提ですが、逆にまったく過去の情報が
ない場合は、それぞれが均等な確率で
実行されると仮定して下記のように
します。
これを「理由不十分の原則」といいます。
2. 相手が各戦術を取った場合の得点率を定義する
戦術1~4によって得点したという条件を
とし、その確率を
~
とします。これは統計学では尤度と呼ばれ、
各戦術がどれだけ得点に結びつきやすい
かという信頼度のようなものです。
全部の得点回数に対する、各戦術実行
時の得点回数の割合として下記のよう
になります。
3. 相手のトータルでの得点確率を定義する
ここまでの1と2で定義した事前確率と
尤度を利用して、戦術の全パターンを
考慮したトータルの得点確率を
定義します。
戦術1~4を全て考慮するとして、下記の
ように計算出来ます。
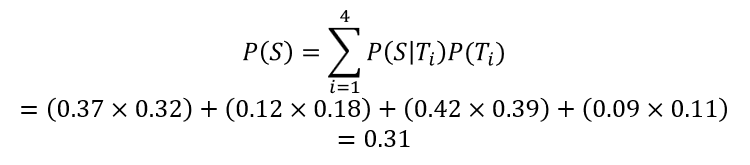
4. 相手が各戦術を取る確率を更新する
前述した1~3にて定義した確率の値を
ベイズの定理に当てはめる事で、
各戦術を相手が取るであろう確率を
下記のように更新します。

ここで、事前に定義した各戦術の
確率~
の値と
比べてみましょう。
- 戦術1: 0.32 -> 0.38
- 戦術2: 0.18 -> 0.07
- 戦術3: 0.39 -> 0.52
- 戦術4: 0.25 -> 0.03
それぞれの戦術を相手が取る確率が
更新前と後で変化している事が
分かります。
これは、相手の過去の戦術の実行
確率とそれによる得点確率を考慮
する事で、過去の実施確率と得点
確率が最も高い戦術3を取る確率が
より高いだろうと、自分の予測を
改めた事を意味します。
逆に、過去の実施確率も得点確率
も低い戦術2や4を相手が取る確率
は低いだろうという事で、事前より
さらに低い確率で見積もるように
なります。
5. 各戦術における自分の得点確率を事前定義する
相手が取るであろう戦術を予測する
と同時に、自分が取るべき戦術も
考えなければなりません。
この場合、得点が出来る確率が
一番高い戦術を選択するのが
自然なので、ここで推定したい
のは、各戦術を実行した時に
得点できる確率とします。
まずは事前確率として、どの
戦術とかは関係なしに、自分が
相手から得点できる確率と、
相手から失点する確率を
定義します。
相手との過去の戦績から決める
事もできますが、ここでは
得点する確率も失点する確率も
イーブンだと考える状態から
始めます。よって、
とします。
6. 自分の得失点時に各戦術を取った確率を定義する
続いて尤度として、自分が得点
あるいは失点した際に、どの
戦術を取った確率が高かった
のかを考えます。
まずは、自分が過去に得点した
際に各戦術を取った確率です。
続いて、自分が過去に失点した
際に各戦術を取った確率です。
7. 自分がトータルで各戦術を取った確率を定義する
得点した場合と失点した場合の
両方を考慮して、各戦術を取った
確率を下記のように定義します。
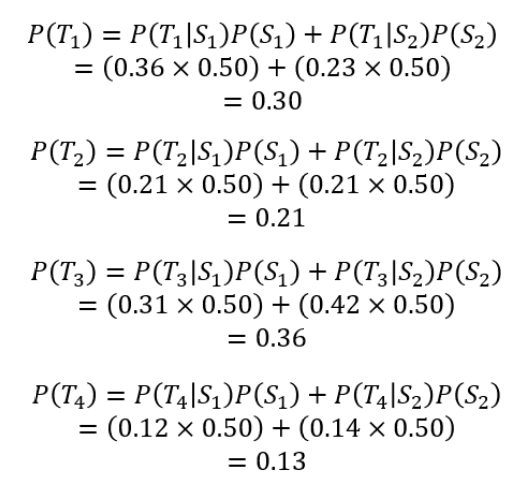
8. 各戦術を取った場合の得点確率を推定する
前述した5~7で定義した各種
確率をベイズの定理に当て
はめて、各戦術を実行したら
どれくらいの確率で得点出来る
かを推定します。
推定結果は下記の通りになります。
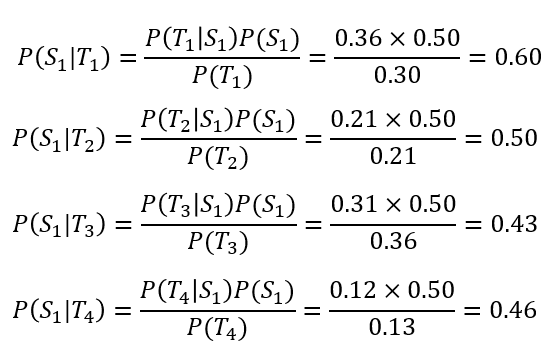
事前には、得点確率は失点確率と
イーブンで0.5としたのと、この
推定結果を比べてみましょう。
- 戦術1: 0.5 -> 0.6
- 戦術2: 0.5 -> 0.5
- 戦術3: 0.5 -> 0.43
- 戦術4: 0.5 -> 0.46
戦術1が一番得点出来る確率が
高いという事になっていますね。
戦術1の実行確率は全体の30%
ですが、得点した場合だけに
限定すると、4つの戦術の中で
一番実行確率が高い36%です。
この事から、戦術1を実行した
方が一番得点しやすいとされ、
元々の想定である50%よりも
少し高めの60%に確率を見積り
直したという事なります。
今後の取り組み
卓球の試合分析にベイズの定理を
応用する感覚が掴めました。
Tリーグのスタッツを見てみると、
各ゲームの勝率やその時点での
点差などもまとめられていました。
これらも利用して、試合の流れを
より高精度に予測できないかを
次回は考えてみようと思います。