目次
背景・目的
自動車の運動学を理解するための物理基礎の勉強メモとして、
前回の記事では直線運動に関するものを書きました。
今回は回転運動に関する記事を書いていきます。
参考ブログ
回転運動における物理量
ハンドル、タイヤ、ステアリング、車両の旋回運動などは、
その物体上あるいは空間上のある一点を中心とした回転運動を
します。それに関わる物理量には、下記のようなものがあります。
角度
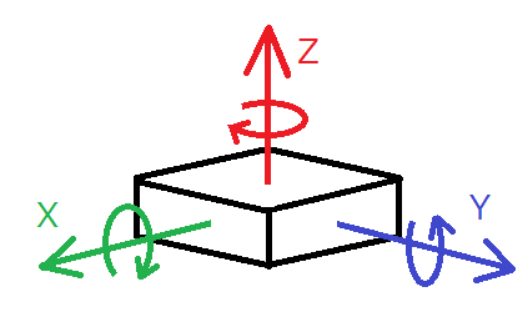
下記の図でに当たるのが角度になります。
単位にはdeg、またはradが使われます。

自動車の制御における角度データとしてまず思い浮かぶのは、
加速度センサやジャイロセンサから得られる姿勢データでしょう。
こちらの記事で解説されているように、X, Y, Zの3軸方向の加速度
からそれぞれの方向における傾き角度を求めることができます。
sites.google.com
Circular(サーキュラー)という角度の単位
プログラムの中で角度データを処理する際、sinやcosのような
三角関数の計算をする事が多いので、単位は[rad]にしておく
方が都合はいいです。この時、センサの仕様次第ではありますが、
角度データの分解能は0.1[deg]や0.01[deg]であることが多いでしょう。
また、こういったセンサから得られる信号データの分解能はビットと
という単位で表現されるので、例えばセンサからのデータのサイズが
16ビットであれば、取り得る値の範囲を16ビットで分割した、
より細かい単位に変換する場合もあります。
センサの取り得る値の範囲±180[deg]で16ビットサイズであった場合、
16ビットが取り得る最大の値が65535であることから、180/65535[deg]
であり、それは0.0027[deg]であり、0.1[deg]や0.01[deg]よりも更に
細かい分解能として扱えるようになります。
角速度
物が回転する速さを表し、数式上ではギリシャ文字のω(オメガ)が
使われます。単位はrad/sになります。また、この
角速度を2π[rad]で割ったものを周波数といい、1秒間に何回転するか
を表す物理量となります。単位はHzです。さらに、周波数の
逆数をとったものは周期といい、1回転にかかる時間を表します。
mathwords.net
角速度を用いた姿勢角の推定
3次元の角速度を計測するセンサとしてジャイロセンサがありますが、
これは加速度センサに比べて高周波で細かい動きを検知するのが得意
なセンサとされており、ロボットや自動車の姿勢角を推定するのには
ジャイロセンサを用いる場合の方が多いようです。
ただし、ジャイロセンサによる姿勢角推定は、誤差が蓄積したりゼロ点が
オフセットする(ドリフト)するといった問題もあるので、それらを打ち消す
ような工夫が必要になります。
ジャイロセンサの特徴や弱点、姿勢角推定までの理論の導出などは、下記
の記事で詳しく紹介されています。
watako-lab.com
角運動量
並進運動における運動量に対応するのが角運動量です。
運動の勢いの程度を意味するのが運動量であり、角運動量は回転運動の
勢いとみなすことが出来ます。以下の図のように、物体が運動量Pで
回転運動しているとすると、回転半径rとPの外積が角運動量になります。

近年では、ドライバの体の重心周りにおける角運動量に着目して、
運転中の姿勢保持動作を分析する手法が研究されていたりします。
https://www.jstage.jst.go.jp/article/jsaeronbun/50/2/50_20194259/_pdf
慣性モーメント
回転運動における運動量Pは、回転速度がとなることより、
運動量P=mr2ωとなり、この式におけるmr2の部分が慣性モーメントに
なります。自動車の運動学では、車の姿勢を論じる際に、車が回転しやすいか否かを
表す物理量が慣性モーメントです。

慣性モーメントの計算式から分かるように、回転する物体と中心との距離が近いほど
慣性モーメントは小さい、つまり回転しやすいという事になります。これを自動車に
当てはめると、車体の重心が回転中心に近い方が俊敏に回転するようになります。
慣性モーメントを考慮した車体の設計
飛行機では3軸それぞれの慣性モーメントについて配慮する必要があるのに対して、
自動車では基本的に水平面上を走ると仮定して、ヨー軸まわりの慣性モーメントだけを
考慮して設計されるようです。
このとき、ヨー軸を車体上のどこに設定するかが操作性に大きく影響すると
言われています。これについては、下記の記事で詳しく説明されています。
www5.plala.or.jp
力のモーメント(トルク)
トルクは物体を回転させる力であり、単位はNmとなります。
トルクは下記の図のように、回転円の半径×円の接線方向の力で求まります。例えば
ブレーキによって車が止まろうとする場合、進行方向と同じ方向に回転しているタイヤ
を、ブレーキによる制動力が回転しているのと逆の方向に作用して、タイヤの回転を
止めようとします。このトルクをブレーキトルクと呼んだりします。

また、トルクに1秒当たりの回転数をかけたものは仕事率になり、これがいわゆる馬力
となります。車のスペックを表す項目として最高出力や最大トルクがありますが、
出力が馬力にあたります。出力とトルクはお互いが密接に関係しており、それは
下記の記事にて詳しく説明されています。
http://qa.jaf.or.jp/mechanism/engine/05.htmqa.jaf.or.jp
遠心力
遠心力とは、円周上を回っている物体が外側に膨らもうとする力です。
遠心力を求める式は、質量×回転半径×角速度2、つまりmrω2となります。
また、式中のrωは回転速度vなので、mv2/rという形でも求める事ができます。
車が旋回するときは、下図のように車体の重心に遠心力がかかります。これだけだと
車体は外側にどんどん膨らんでしまいますが、各タイヤに対して回転の内側に生じる
コーナリングフォースとの釣り合いによって、外側に膨らまず一定の旋回状態を
維持するようになります。これを定常円旋回といいます。
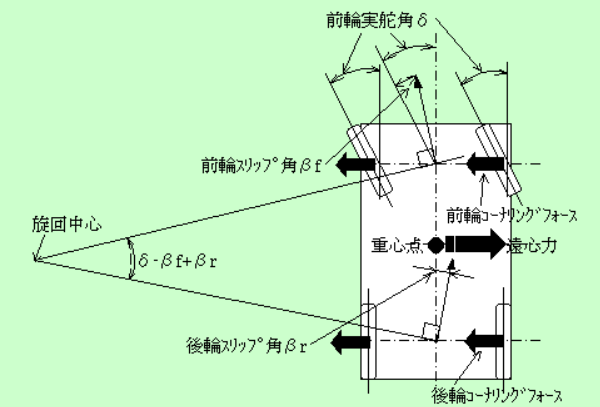
タイヤにかかる横力とコーナリングフォース
旋回直前まで車両が進んでいた進行方向に対して、ハンドル操作によりタイヤの
向きとの間に生じる角度ずれをスリップ角といいます。それによりタイヤ縦方向の
力と横方向の力
が発生します。この横方向の力は横力と言われ、
横力の内の「進行方向に対する直角成分」がコーナリングフォースです。

車両が旋回していくことで前輪と後輪にそれぞれコーナリングフォースが加わり、
これらと遠心力が釣り合うことにより、車両はスピンしたりせず一定の旋回状態を
キープできるようになるという訳です。
この辺の詳しい説明は、下記の記事にて紹介されています。
www5f.biglobe.ne.jp
www5f.biglobe.ne.jp
