はじめに
前回の投稿から間が空いてしまいましたが、また下記の書籍を読みながら、機械学習に必要な数学の基礎について勉強を再開しました。

- 作者: 伊藤真
- 出版社/メーカー: 翔泳社
- 発売日: 2018/01/24
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (3件) を見る
今回の記事では、指数関数・対数関数について勉強した際にメモしたことを書いていきます。
前回までの記事
前回までに書いた、「ベクトルと微分編」「行列編」は下記になりますので、合わせてどうぞ。
指数関数とは
指数関数は、の形で定義される関数である。これは、「aを底とする指数関数」と言われる。また、この式をグラフで描くと下記のようになる。
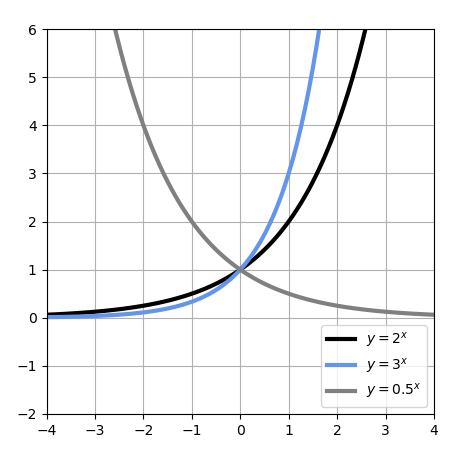
a > 1の時は単調増加のグラフになり、0 < a < 1のときは単調減少のグラフになる。出力は常に0よりも上になるので、指数関数は、負の数でも正の数でも、全てを正の数に移す関数と言える。
対数関数とは
対数関数は、指数関数の入力と出力を逆にしたもの、つまり、指数関数の逆関数である。という数式を考え、これをy=の形に変形すると
となり、グラフで描くと下記のようになる。
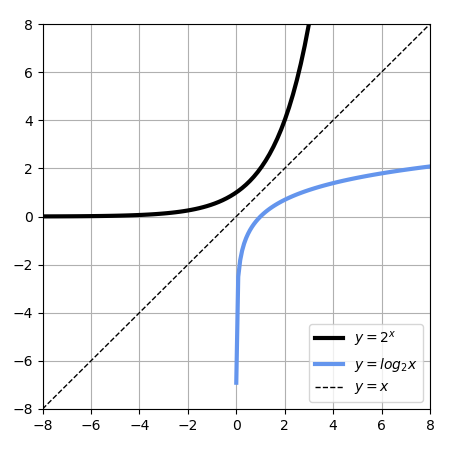
これを見ると、と
のグラフが
の線で対称になっていることが分かる。また、xが大きくなればなるほどグラフは増加するが、その傾きはどんどんなだらかになる。
対数の便利さ
aが底の対数は、大きすぎる数や小さすぎる数を扱いやすい大きさの数にしてくれる。例えば、をa=10の対数で表せば、
となる。
底を明記せずにと書けば、底に
を使ったことになる。
は、
の無理数で、自然対数の底、または、ネイピア数と呼ばれる。
機械学習における対数
機械学習では、非常に大きな数や小さな数を扱うが、プログラムでこのような数を扱うとオーバーフローを起こしてします場合がある。そのような数は、対数をとることで、オーバーフローを防ぐことができる。また、対数は、掛け算を足し算に変換することができる。関数を考えた場合、下記の公式が成り立つ。
特に確率の場合、尤度という掛け算で表された確率は、対数をとった「対数尤度」で考えるのが常套手段となっている。
関数 の最大値、最小値を探す場合
の最大値、最小値を探す場合
ある関数があったとして、その
を最小にする
を求めるとする。この場合、対数をとった
も、同じ
で最小になるが、対数は単調増加関数であるので、最小値は変わっても、最小値をとる値は変わらない。このことをグラフで表すと下記のようになる。
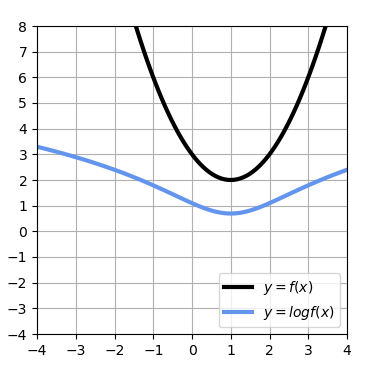
このグラフにおけるは、
であり、
のときに最小値をとる。また、
も
のときに最小値をとる。この特徴を数式で表すと下記のようになる。
この式におけるとは、
が最小値をとるxという意味であり、このグラフの場合は
となる。この性質により、
の代わりに、
を最小にするような
を求めるというテクニックがよく使われる。
指数関数の微分
指数関数のxに関する微分は下記の式のようになる。
この式を見ると分かるように、微分すると、元の式であるに
が掛け算された形となる。これにより、微分する前と後での違いを可視化すると、下記のグラフのようになる。
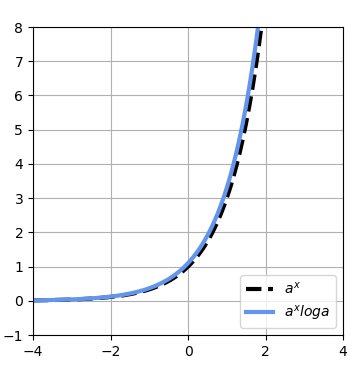
まず、a=2とすると、の値は0.69となるので、微分後のグラフの方が微分前よりも下にくるようになる。
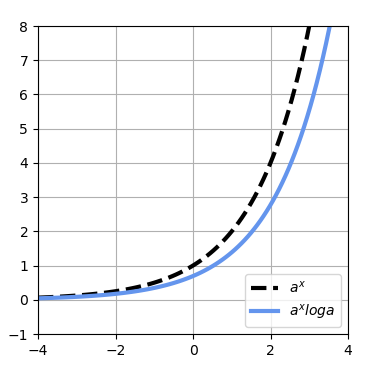 次に、a=3とすると、
次に、a=3とすると、の値は1.09となり、a=2のときよりも値が大きくなる。そのため、下記のように微分後のグラフが微分前よりも上にくるようになる。
ここで特別なのは、a=e(ネイピア数)のときである。となるので、微分した式は
となる。つまり、a=eのときは、下記グラフのように微分前と後で関数の形は変わらないということになる。
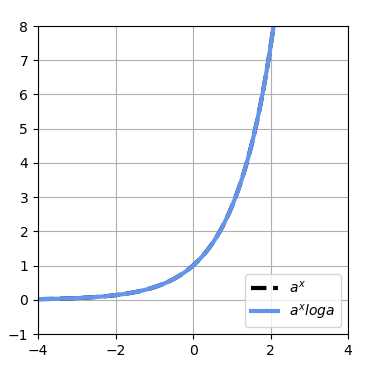
これは、微分の計算をするときにはとても便利な性質である。
対数関数の微分
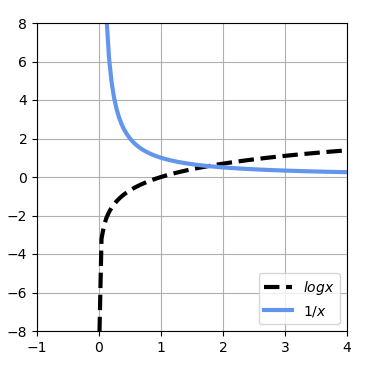
対数関数の微分は、下記のような反比例の式になる。
また、これをグラフにすると下記のようになる。
サンプルコード
ここまで記載した各グラフを作成するPythonのサンプルコードは下記のGitHubリポジトリで公開しています。